| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- python
- 비트코인
- it
- 백트레이더
- Cloud
- 프로그래밍
- 확률
- 토플 라이팅
- AUTOSAR
- 퀀트
- 자동매매
- AWS
- TOEFL
- 블록체인
- 암호화폐
- 개발자
- 아마존 웹 서비스
- 임베디드
- 토플
- 클라우드
- 실시간시스템
- can
- probability
- toefl writing
- backtrader
- 오토사
- realtimesystem
- 파이썬
- GeorgiaTech
- 자동차sw
- Today
- Total
Leo's Garage
Conditionally Optimal Task Parallelization for Global EDF on Multi-core Systems 본문
Conditionally Optimal Task Parallelization for Global EDF on Multi-core Systems
LeoBehindK 2025. 6. 6. 22:02느낀점
Problem Statement
RealTime Task의 "Parallellization freedom"은 OpenCL 및 OpenMP와 같은 최신 병렬 컴퓨팅 프레임워크에서 Task를 여러 가지 방법으로 병렬화할 수 있게 해주는 개념이다. 예를 들어 한 차선 추적 프로그램은 단일 스레드, 두 개의 스레드, 세 개의 스레드, 네 개의 스레드로 실행될 수 있다. 이러한 프레임워크에서는 각 Task 병렬화되는 스레드의 수인 "Prallelization option"을 신중하게 결정해야 다중 CPU 코어를 더 잘 활용하여 스케줄 가능성을 극대화할 수 있다. 이 논문은 특히 Global EDF(G-EDF) 스케줄링 환경에서 Task 병렬화 옵션을 최적으로 할당하는 방법을 제안한다.
병렬화 자유가 G-EDF 환경에서 RealTime Task의 스케줄 가능성에 미치는 영향은 다음과 같다.
- 개별 스레드 실행 시간 및 전체 실행 시간의 변화: Task의 병렬화 옵션을 늘리면 (즉, 더 많은 스레드로 분할하면) 일반적으로 각 스레드의 실행 시간은 줄어든다. 그러나 병렬화 Overhead때문에 모든 스레드의 total computation amount는 증가하는 경향이 있다.
- Task 자체의 스케줄 가능성에 대한 영향(내성 증가): G-EDF에서 Task의 병렬화 옵션이 커지면 (즉, 더 많은 스레드로 병렬화되면) Task 자체의 스케줄 가능성에 유리한 측면이 있다. 이는 가장 긴 실행 시간을 가진 대표 스레드의 실행 시간이 짧아져, 다른 Task의 Interference에 대한 내성(tolerance)이 커지기 때문이다. 이 내성은 병렬화 옵션에 대한 단조 증가(monotonic increasing) 함수의 속성을 가진다. 즉, 병렬화 옵션이 커질수록 Task가 다른 Task로부터 받을 수 있는 Interference의 양이 커진다.
- 다른 Task에 대한 스케줄 가능성에 대한 영향 (간섭 증가): 반면에, Task의 병렬화 옵션을 늘리는 것은 다른 Task에게는 불리할 수 있다. 병렬화된 Task의 스레드들이 다른 Task의 스레드들에게 더 큰 Interference을 생성할 수 있기 때문이다. 이 Interference 함수 또한 병렬화 옵션에 대한 단조 증가 함수의 속성을 가진다. 즉, Task의 병렬화 옵션이 커질수록 다른 Task에게 주는 Interference의 양이 더 커진다.
- 내성 대 간섭의 Trade Off: 결과적으로 Task의 병렬화 옵션을 늘리는 것은 내성을 증가시켜 Task 자신의 스케줄 가능성에 유리하지만, 다른 Task에게 주는 Interference을 증가시켜 전체 시스템의 스케줄 가능성에는 불리할 수 있는 Trade Off 관계를 발생시킨다. G-EDF 스케줄링 하에서 Task Set의 스케줄 가능성은 각 Task의 내성이 다른 모든 Task로부터 받는 총 Interference보다 크거나 같을 때 보장될 수 있다.
이러한 내성과 간섭의 단조 증가 속성을 활용하여, 본 논문에서 제안하는 알고리즘은 모든 Task에 대해 최소 병렬화 옵션에서 시작하여, 각 Task의 내성이 다른 Task로부터 받는 Interference보다 겨우 커지는("barely tolerable")옵션으로 반복적으로 증가시키는 방식으로 최적의 병렬화 옵션 조합을 찾는다.
이 논문은 multi-core 시스템에서 global-EDF (Earliest Deadline First) 스케줄링을 사용할 때, 병렬화 자유도(Parallelization freedom)를 가진 Task들의 병렬화 옵션을 어떻게 선택할 것인가에 대한 문제를 다룬다. 각 Task는 여러 개의 스레드로 병렬화될 수 있고, 각 병렬화 옵션은 Task의 실행 시간 및 스케줄러에 미치는 Interference에 영향을 준다.
목표는 모든 Task가 Deadline을 지키도록 하면서 가능한 최적의 병렬화 옵션을 할당하는 것이다.
Contribution
- 병렬화 자유도를 고려한 G-EDF 스케줄링 하에서의 Conditional Optimal Task Parallelization 할당 알고리즘 제안
- BCL(Bertogna, Cirinei, and Lipari)분석을 기반으로 tolerance와 interference 함수의 단조 증가 성질을 도출
- 이를 기반으로 다항 시간 내 조건부 최적 알고리즘을 제안
- 실험을 통해 기존 방식 대비 최대 60% 스케줄러 성공률 향상 확인
Key Ideas
- 각 Task는 다양한 스레드 개수로 병렬화할 수 있고, 병렬화 옵션에 따라 실행 시간 및 간섭이 달라진다.
- Interference은 다른 Task의 실행으로 인해 특정 Task가 지연되는 시간이다.
- Task의 병렬화 옵션을 높이면 자신의 실행 시간은 줄어들고 간섭을 더 잘 견디게 되지만, 다른 Task에 더 많은 Interference을 유발한다.
- 이러한 trade-off를 반영해 각 Task의 tolerance 함수와 interference 함수를 정의하고, 이 함수들의 단조 증가 성질을 이용해 one-way iterative algorithm으로 최적 옵션을 할당한다.
Mathematics View (Lemmas & Theorems)
Lemma 1 : 대표 스레드($\tau_{1k}$)가 schedulable하면 모든 sibling도 schedulable하다.
정리: 만약 병렬화된 Task $\tau_k(O_k)$의 첫번째 (최대 WCET를 갖는) 스레드 $\tau_{1k}(O_k)$가 BCL Schedulability 조건을 만족하면, 나머지 sibling 스레드들도 모두 해당 조건을 만족한다.
증명:
- $\tau_k$의 병렬화된 스레드 집합은 $\tau_k(O_k)=\{ \tau_{1k}(O_k), \tau_{2k}(O_k), ... , \tau_{O_k}(O_k) \}$
- 이 중 $\tau_{1k}(O_k)$는 가장 큰 WCET(Worst Case Execution time)를 가짐 -> $e_1^k(O_k) \geq e_l^k(O_k), \,\,\,\forall l$
- BCL 조건:
-
- $$\sum_{\tau_i\neq \tau_k}^{}min(W_{\tau_i,\tau_1^k},D_k-e_1^k(O_k))+min(W_{\tau_k^*,\tau_1^k},D_k-e_1^k(O_k))\leq m(D_k-e_1^k(O_k))$$
-
- sibling인 $\tau_{lk}(O_k)$는 동일한 Release/Deadline을 가지므로 workload는 동일하지만, $e_l^k(O_k)<e_l^k(O_k)$
- 따라서, $D_k-e_l^k(O_k)>D_k-e_1^k(O_k)\Rightarrow interference$에 대한 허용량(tolerance)이 더 큼
- 간섭량이 동일하거나 감소하므로, $\tau_{lk}(O_k)$도 조건을 만족
직관:
- sibling 스레드들은 동시에 시작하고 동시에 끝남
- 따라서 가장 오래 걸리는 $\tau_{1k}$만 스케줄 가능하면, 나머지도 여유롭게 실행됨
- 마치 "물병에 가장 큰 돌이 들어가면, 나머지 자갈도 들어간다"는 원리
Lemma 2 : Tolerance 함수는 단조 증가한다.
정리: 병렬화 옵션 $O_k$가 증가하면, 해당 Task $\tau_k$의 interference tolerance는 증가한다.
즉, $W_{tolerance}^{\tau_k}(O_k)<W_{tolerance}^{\tau_k}(O_k+1)
수학적 정의:
$$W_{tolerance}^{\tau_k}(O_k)=m(D_k-e_1^k(O_k))-\sum_{l=2}^{O_k}min(e_l^k(O_k),D_k-e_l^k(O_k))$$
증명:
- 병렬화 수준 $O_k$ -> $O_k+1$로 증가
- $e_1^k(O_k+1) < e_1^k(O_k)$ -> 첫 스레드 실행 시간 감소
- $D_k-e_1^k$증가 -> 첫 항 $m(D_k-e_1^k)$ 증가
- Sibling 간섭함 (두번째 항)은 일부 증가할 수 있으나 제한적:
- 증가량 $ \leq C_k(O_k+1) - C_k(O_k) + O_k(e_1^k(O_k)-e_1^k(O_k+1))$
- 증가한 sibling 수 만큼의 최대 증가량
- 전체적으로 첫 항의 증가량이 두 번째 항의 증가량을 초과
- 전체 tolerance 증가
직관:
- 병렬화하면 작업량이 쪼개지므로 긴 스레드가 짧아짐 -> "더 빨리 끝날 수 있음"
- 간섭을 견디는 능력(tolerance)이 향상됨
- 마치 칼을 여러 개 들고 싸우는 병사가 혼자 싸우는 병사보다 더 버티는 것 처럼
Corollary 1 : 일정 오버헤드 조건에서 Lemma 2 유지됨
정리: 병렬화 Overhead $\alpha(O_k, O_k+1)<m-O_k$이면 tolerance는 여전히 증가
정의:
$$\alpha(O_k,O_k+1)=\frac{C_k(O_k+1)-C_k(O_k)}{e_1^k(O_k)-e_1^k(O_k+1)}$$
증명:
- tolerance 증가량 $ \geq m(e_1^k(O_k)-e_1^k(O_k+1))$
- 두 번째 항 증가량 $ \leq (\alpha+O_k)(e_1^k(O_k)-e_1^k(O_k+1))$
- 따라서 $\alpha+O_k < m$이면 증가량이 유지됨
직관:
- 병렬화의 효율이 너무 낮지만 않으면(tolerable overhead), 전체 성능은 여전히 증가
Lemma 3 : Interference 함수도 단조 증가
정리: $\tau_k$의 병렬화 옵션 $O_k$가 증가할 수록, 다른 Task $\tau_i$에 주는 간섭량도 증가함
즐, $W_{interference}^{\tau_k \to \tau_i}(O_k)$은 단조 증가 함수
수식:
$$W_{interference}^{\tau_k,\tau_i}(O_k)=\sum_{l=1}^{O_k}min(W_{\tau_k^l,\tau_i^1},D_i-e_1^i)$$
각 thread interference:
$$W_{\tau_k^l,\tau_i^1}=\left \lfloor \frac{D_i}{T_k}\right \rfloor e_l^k(O_k)+min(e_l^k(O_k),D_i \,\,\, mod \,\, T_k)$$
증명:
- 스레드 수 증가 -> 간섭 항 수 증가
- 각 $e_l^k$는 감소하지만 수가 많아지므로 전체 합은 증가함
- Carry-In Job의 간섭도 늘어남
직관:
- 스레드가 많아질수록 더 자주 CPU를 차지하므로, 다른 Task가 덜 실행될 수 있음
- "일을 쪼갠 만큼, 남에게 방해되는 순간이 많아짐"
Algorithm 1 - OPAP Algorithm
Algorithm OPOA (Optimal Parallelization Option Assignment)
Input:
- Task set Γ = {τ₁, τ₂, ..., τₙ}
- Each τₖ has (Tₖ, Dₖ, Eₖ[1..Omax]) // 주기, 마감시간, 병렬화 옵션별 실행시간
- Number of cores: m
Output:
- For each task τₖ, selected parallelization option Oₖ ∈ [1, Omax]
- Whether the task set is schedulable under global EDF
----------------------------------------------------------------
1: for each task τₖ ∈ Γ do
2: for each option Oₖ = 1 to Omax do
3: compute tolerance W_tolerance[τₖ][Oₖ] using Eq.(10)
4: end for
5: end for
// 초기화: 각 병렬화 옵션에 대해 해당 태스크가 허용할 수 있는 최대 간섭량 계산
6: initialize current option O_cur ← [1, 1, ..., 1] // 모든 태스크는 병렬화 안 된 상태로 시작
7: set updated ← true // 반복 루프를 시작하기 위한 플래그
8: initialize schedulability status S ← [Unknown, ..., Unknown] // 각 태스크의 스케줄 가능 여부
9: while updated == true do
10: updated ← false // 루프 종료 조건: 어떤 태스크도 옵션이 바뀌지 않으면 종료
11: O_prev ← O_cur // 이전 옵션 백업
12: for each task τₖ ∈ Γ do
13: compute total interference from all other tasks:
Iₖ ← ∑_{i ≠ k} W_interference[τᵢ → τₖ] using Eq.(12)
14: while W_tolerance[τₖ][O_cur[k]] < Iₖ do
// 현재 병렬화 옵션에서 간섭을 견딜 수 없으면
15: O_cur[k] ← O_cur[k] + 1
16: updated ← true // 업데이트가 발생했으므로 다음 반복 필요
17: if O_cur[k] > Omax then
18: S[k] ← False // 최대 옵션까지 올렸지만 여전히 간섭을 못 견딤
19: break // 이 태스크는 더 이상 조정 불가
20: end if
21: end while
22: end for
23: if any S[k] == False then
24: break // 하나라도 스케줄 불가능한 태스크가 있으면 반복 중단
25: end if
26: end while
27: if any S[k] == False then
28: return "Not schedulable"
29: else
30: return "Schedulable", O_cur
31: end if
| 핵심요소 | 설명 |
| Tolerance | 태스크가 외부 간섭을 얼마나 견딜 수 있는지 (↓실행시간, ↑허용간섭) |
| Interference | 다른 태스크들이 해당 태스크에 유발하는 간섭량 |
| 단조 증가성 활용 | tolerance와 interference 모두 병렬화 옵션에 따라 단조 증가 → one-way 탐색 가능 |
| updated 플래그 | 한 번이라도 옵션이 바뀌면 다음 iteration 필요 |
| Barely tolerable 선택 | 각 태스크에 대해 간섭을 겨우 견딜 수 있는 최소 병렬화 옵션을 선택 |
: 이 알고리즘은 최적화 탐색 없이도 병렬화 옵션 공간을 다항 시간 내에서 탐색할 수 있는 핵심 설계이며, 실시간 시스템에서 빠르게 병렬화 조정을 하기 위한 매우 실용적인 접근이다.
Theorem 1 : Algorithm 1의 조건부 최적성 보장
정리: 병렬화 오버헤드가 작으면 ($\alpha<m-O_k$), Algorithm 1은 BCL 분석에 대해 최적이다.
즉, Algorithm 1이 해를 찾지 못하면, 어떤 다른 병렬화 조합도 BCL 기준에서 해를 찾을 수 없다.
핵심아이디어:
- Option Space를 One-way로 탐색
- tolerance 함수는 단조 증가, interference도 단조 증가
- 더 낮은 옵션은 간섭을 못 견디고, 더 높은 옵션은 간섭을 더 유발
증명:
- 알고리즘은 최소 옵션 (1,1,...,1)에서 시작해 iteratively 올림
- 모든 $\tau_k$에 대해 Barely tolerable 옵션으로 업데이트
- 어떤 옵션에서도 Schedulable하지 않으면, 그 어떤 조합도 불가능
직관:
- 가장 낮은 수준부터 올리며 "필요한 만큼만 병렬화"
- 더 병렬화하면 간섭이 증가하여 전체 시스템에 불리
- 마치 "꼭 필요한 만큼만 무장을 하되, 과도하면 오히려 피해"와 유사
OPAP 알고리즘 파이썬으로 구현
import matplotlib.pyplot as plt
# ----------------------------
# Task Configuration (병렬화 필수 예제)
# ----------------------------
tasks = [
{'T': 1000, 'D': 400, 'maxOption': 4, 'E': [0, 500, 260, 180, 130]}, # Task 0
{'T': 900, 'D': 300, 'maxOption': 4, 'E': [0, 450, 230, 160, 120]}, # Task 1
{'T': 1100, 'D': 350, 'maxOption': 4, 'E': [0, 480, 240, 170, 125]} # Task 2
]
n = len(tasks) # number of tasks
m = 4 # number of cores
Ok = [1] * n # initial parallelization options
# ----------------------------
# Helper Functions
# ----------------------------
def get_tolerance(k, ok):
"""Calculates tolerance for task k at option ok (Eq. 10)"""
Dk = tasks[k]['D']
e1 = tasks[k]['E'][ok]
tolerance = m * (Dk - e1)
for l in range(1, ok):
el = tasks[k]['E'][l]
bound = Dk - e1
tolerance -= min(el, bound)
return tolerance
def get_interference(from_task, to_task, oi):
"""Calculates interference from τ_from to τ_to (Eq. 12 approx)"""
ei = tasks[from_task]['E'][oi]
Ti = tasks[from_task]['T']
Di = tasks[to_task]['D']
carry_in = min(ei, Di % Ti)
sum_work = (Di // Ti) * ei + carry_in
bound = Di - tasks[to_task]['E'][Ok[to_task]]
return min(sum_work, bound)
def is_schedulable(k):
"""Checks schedulability of task k using current Ok values"""
tol = get_tolerance(k, Ok[k])
interference = sum(get_interference(i, k, Ok[i]) for i in range(n) if i != k)
return interference <= tol
def OPOA():
"""Optimal Parallelization Option Assignment algorithm"""
updated = True
history = []
while updated:
updated = False
history.append(Ok[:])
for k in range(n):
while not is_schedulable(k):
if Ok[k] + 1 > tasks[k]['maxOption']:
return False, history
Ok[k] += 1
updated = True
return True, history
# ----------------------------
# Run the Algorithm
# ----------------------------
result, history = OPOA()
# ----------------------------
# Print Results
# ----------------------------
if result:
print("Schedulable. Final parallelization options (O_k):")
for i, o in enumerate(Ok):
print(f"Task {i}: O_k = {o}")
else:
print("Not schedulable with any option.")
# ----------------------------
# Plot History of Parallelization Options
# ----------------------------
fig, ax = plt.subplots()
for i in range(n):
values = [step[i] for step in history]
ax.plot(range(len(history)), values, marker='o', label=f'Task {i}')
ax.set_title("Parallelization Option Assignment (Hard Real-Time Case)")
ax.set_xlabel("Iteration")
ax.set_ylabel("Parallelization Option (O_k)")
ax.set_yticks(range(1, 5))
ax.set_xticks(range(len(history)))
ax.legend()
plt.grid(True)
plt.tight_layout()
plt.show()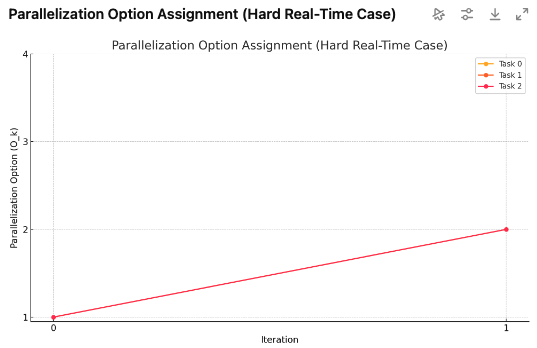
결과 요약:
- 세 개의 Task 모두 병렬화 옵션 $O_k=2$ 이상이 안니면 Deadline을 맞출 수 없었다.
- 따라서 알고리즘은 자동으로 각 Task의 병렬화 수준을 올려서 Schedulabillity를 확보했다.
그래프 해석:
- 세 개의 Task 모두 병렬화 옵션 $O_k=1$에서 시작하지만, interference > tolerance 조건을 만족하지 못해 옵션을 증가
- iteration을 통해 점차적으로 필요한 병렬화 수준에 도달
REF
Y. Cho, D. H. Kim, D. Park, S. S. Lee, and C. G. Lee, "Conditionally Optimal Task Parallelization for Global EDF on Multi-core Systems," 2019 IEEE Real-Time Systems Symposium (RTSS), Hong Kong, China, 2019, pp. 194–207, doi: 10.1109/RTSS46320.2019.00027.
