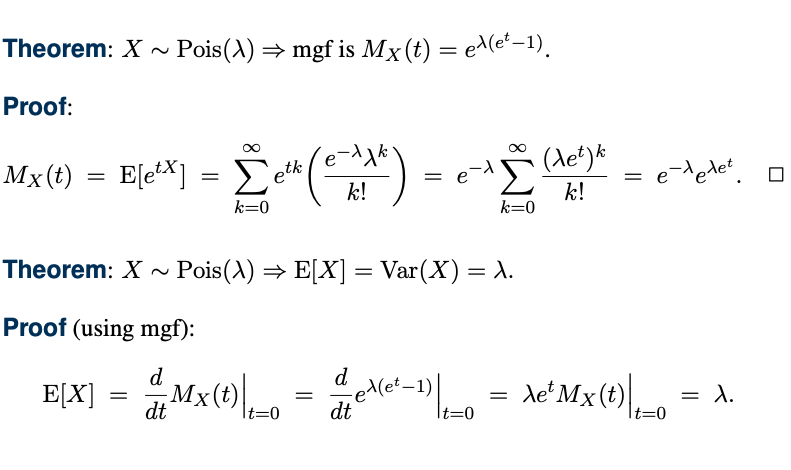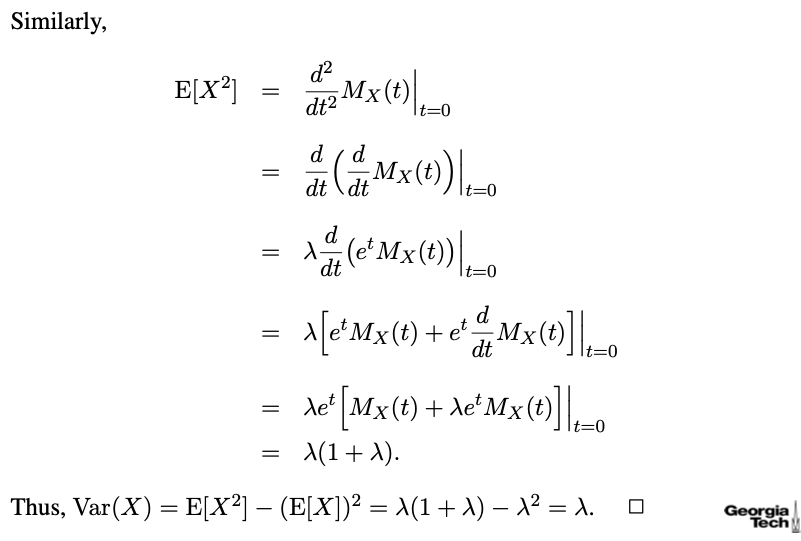| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- can
- 토플 라이팅
- 토플
- 블록체인
- AUTOSAR
- TOEFL
- 자동매매
- 파이썬
- 자동차sw
- probability
- AWS
- 아마존 웹 서비스
- Bitcoin
- backtest
- 오토사
- 비트코인
- 백테스트
- toefl writing
- python
- 확률
- GeorgiaTech
- 클라우드
- 퀀트
- 개발자
- 암호화폐
- 프로그래밍
- backtrader
- Cloud
- it
- 백트레이더
- Today
- Total
Leo's Garage
Probability and Statistics III: A Gentle Introduction to Statistics - 4 본문
Probability and Statistics III: A Gentle Introduction to Statistics - 4
LeoBehindK 2024. 1. 28. 22:27Poisson Distribution

N(t)는 발생한 어떤 사건의 수를 의미하며 t에 대한 함수이다.
이 t는 시간일 수도 있고, 길이나 부피일 수도 있다.
Lamda는 단위 시간 혹은 길이,부피에 대한 사건이 발생할 평균값이다.
여기서 Counting Process는 t동안 발생하는 사건의 수에 대한 확률 과정이다.
말이 좀 어색한데 예를 들어 1시간에 오는 버스의 수도 Counting Process라고 할 수 있다.

푸아송 과정은 t시간 동안에 발생하는 사건의 수를 나타내는 확률과정인데 정상성과 독립성을 만족하면서, 초기 사건의 수가 0번이고, 발생할 사건의 수가 푸아송 분포를 따라야 한다.
1번 문장의 첫번째 식을 살펴보자.
충분히 작은 시간구간 h에서 사건이 0회 발생할 확률은 다음과 같다.
h가 충분히 작으므로 o(h)는 무시할 수 있고 Lamda*h만큼의 확률을 제외한 확률을 가지게 된다.
1번 문장의 두번째 식을 살펴보자.
충분히 작은 시간구간 h에서 사건이 1회 발생할 확률은 다음과 같다.
o(h)는 h로 미분할 때, h가 0인 지점에서 기울기 0을 가지는 함수를 나타내는 기호이다.
이는 h가 충분히 작은 값을 가질 때, o(h)는 무시 가능하다고 볼 수 있게 된다.
h가 충분히 작을 때, o(h)를 무시하면, 사건 발생확률은 시간의 폭 h에 비례한다.
1번 문장의 세번째 식을 살펴보자.
충분히 작은 시간구간 h에서 사건이 2회 발생할 확률은 o(h)이다.
h가 충분히 작다면, 사건 발생횟수가
첫번째 내용을 살펴보면,
정상성이란 두 시점 사이에서 일어나는 사건의 발생횟수가 두 시점간의 시간 폭에만 의존하는 경우를 의미한다.
독립성이란 서로 다른 시간 구간에서 일어나는 사건의 발생횟수가 서로 연관이 없는 경우를 의미한다.

위 수식을 말로 풀어서 설명하면 위와 같다.