| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 토플 라이팅
- 파이썬
- 오토사
- backtrader
- 프로그래밍
- 자동차sw
- AWS
- 백트레이더
- 퀀트
- Bitcoin
- GeorgiaTech
- 확률
- 백테스트
- python
- 비트코인
- 블록체인
- AUTOSAR
- 개발자
- probability
- can
- it
- 아마존 웹 서비스
- Cloud
- 토플
- 클라우드
- backtest
- toefl writing
- 암호화폐
- TOEFL
- 자동매매
- Today
- Total
Leo's Garage
Newton's method 본문
어떤 함수의 근을 빠르게 구하는 방법은 어떤 방법이 있을까?
함수 g(x)가 있다고 하자.
가장 쉽게 생각해보면, l, u 라고 하는 임의의 두 수에 대해서 g(l) * g(u) < 0이라면, 해당 두 수 사이에 해가 존재한다고 할 수 있다.
이때 이 l과 u의 값을 점차 좁혀나가면 해를 찾을 수 있을 것 이다.
이러한 기법을 IVT(Intermediate Value Theorem)이라고 한다.
이 IVT 방법을 이용하여 l + u / 2 값을 r값으로 하고 l과 u를 변경해가면서 해를 찾아가는 방식을 Bisection이라고 한다.
말 그대로 l과 u에 대한 g(u)* g(l) < 0 일 때, l과 u 의 중간값에 대한 g(r) 값의 부호가 어디냐에 따라서 l과 u 중 하나를 변경할 수 있다.
하지만 이 방법보다 더 빠르게 근을 찾는 방법이 있다.
바로 Newton's method이다.
Newton's method의 핵심은 f'(a)가 x = a에서의 접선의 기울기라는 기하학적인 미분 해석을 이용한다.
우리가 어떤 함수 f(x)의 근을 전혀 모르는 상황일 때, 특정한 a라는 위치에서 함수의 값을 살펴본다고 하다.
만약에 f(a) >0이면서, 동시에 f'(a) > 0이라면 f(x) = 0인 지점은 a라는 값보다는 작은 쪽에 위치할 가능성이 높다.
그런데 문제는 그러면 이 a라는 값에서 얼마만큼 이동해야 이 함수의 해를 빠르게 찾을 수 있는지 일 것이다.
일반적으로 f(a)값이 크다면 해가 멀리 있다고 볼 수 있을 것이고, f'(a)의 기울기가 크다면, 해가 가까이 있다고 볼 수 있다.
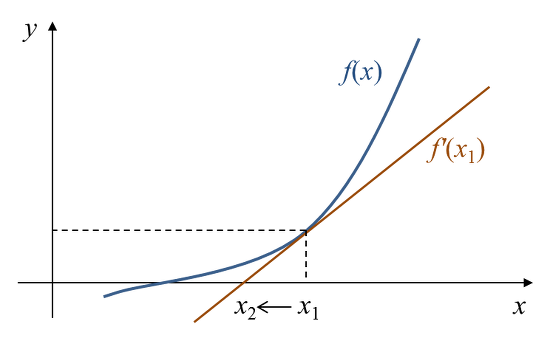
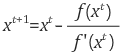
따라서 x의 값은 이전 x의 값에 대해서 현재 f(x)값 나누기 f'(x)의 차를 업데이트 해주는 식으로 변경한다.
다만, 이 Newton's method의 한계는 반드시 함수가 미분가능해야 한다는 점이며, 해는 찾을 수 있더라도 해가 여러 개인 경우는 초기값에 따라서 찾지 못할 수 도 있다.
'Study > Mathematics' 카테고리의 다른 글
| Convolution (합성 곱) (0) | 2024.09.22 |
|---|

