| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- 아마존 웹 서비스
- GeorgiaTech
- 파이썬
- 임베디드
- 자동차sw
- 블록체인
- 토플
- 토플 라이팅
- 클라우드
- 개발자
- 오토사
- AWS
- 비트코인
- backtrader
- 자동매매
- toefl writing
- Cloud
- 프로그래밍
- TOEFL
- can
- 암호화폐
- 실시간시스템
- realtimesystem
- AUTOSAR
- 확률
- probability
- python
- 백트레이더
- 퀀트
- it
- Today
- Total
Leo's Garage
Priority-Driven Scheduling of Periodic Tasks (Dynamic Priority) - 1 본문
Priority-Driven Scheduling of Periodic Tasks (Dynamic Priority) - 1
LeoBehindK 2025. 6. 8. 22:21EDF
EDF (Earliest Deadline First) Scheduler는 Real Time System에서 널리 사용되는 Dynamic Priority Based Scheduling Algorithm이다. 각 Job의 Deadline에 따라 우선순위를 결정하며, Deadline이 가장 빠른 Job부터 먼저 실행된다.
핵심개념
| 요소 | 설명 |
| 우선순위 결정 기준 | 마감 시간이 가까울수록 우선순위가 높음 |
| 작업(Task) | 실시간 작업: (도착 시간, 실행 시간, 마감 시간) 정보를 가짐 |
| 스케줄링 방식 | 동적(Dynamic): 시간이 지남에 따라 우선순위가 바뀜 |
| 선점 가능성 | 선점형(Preemptive) 구현 가능 – 새로운 작업이 더 이른 마감시간을 가지면 실행 중인 작업을 중단하고 실행 |
장점
- Optimality: 단일 프로세서 환경에서, 모든 작업이 Deadline 내에서 완료 가능한 경우 EDF는 반드시 스케줄링 가능함
- 동적 처리: Job들이 동적으로 도착해도 유연하게 대응 가능
단점
- Overhead: Deadline에 따라 우선순위를 자주 계산하므로 연산 비용이 높아질 수 있음
- 자원 공유 문제: 공유 자원 사용 시 우선순위 역전(Priority Inversion) 가능성
- 실패 시 결과 없음: Deadline을 넘기면 그 Job은 무의미할 수 있어 Hard Real Time System에서 신중히 사용해야 함
Processor Utilization Factor
$$U_{lub}(A)=min_{\Gamma }U_{ub}(\Gamma ,A)$$
- $A$: Task Set 또는 시스템 매개변수
- $\Gamma$: 스켸줄링 알고리즘 또는 Task 스케줄링 전략
- $U_{ub}(\Gamma,A)$: 스케줄링 알고리즘 $\Gamma$에 대해 Task Set $A$에 대해 보장 가능한 최대 CPU 이용률 상한
- $U_{lub}(A)$: 모든 가능한 스케줄링 알고리즘 중에서 Task Set $A$에 대해 가능한 최소 상한 (즉, 최적의 상한) - Least Upper Bound
해석:
Task Set $A$에 대해 어떤 알고리즘을 사용하든 가능한 이용률 상한 중 가장 작은 값을 취한 것이 바로 $U_{lub}(A)$이다.
- 여러가지 스케줄링 알고리즘 $\Gamma$가 있고,
- 각각은 Task Set $A$에 대해 어떤 최대 이용률까지 Deadline 보장을 할 수 있는지 다름
- 그 중 가장 보수적인(작은) 상한선을 선택함으로써 어떤 알고리즘을 선택하더라도 작업이 보장될 수 있는 최소한의 기준을 잡는다.
Theorem: EDF Schedulability Condition
주기적이고 독립적인 n개의 작업 집합이 있을 때, 모든 Deadline이 충족될 필요충분조건은 총 CPU 이용률 $U$가 1 이하 일 때이다.
$$\sum_{i=1}^{n}\frac{e_i}{p_i}\leq 1$$
- $e_i$: 작업 $T_i$의 Execution Time
- $p_i$: 작업 $T_i$의 Period
- $\frac{e_i}{p_i}$: 작업 $T_i$의 CPU 이용률
- 전체 이용률 $U=\sum_{i=1}^{n}\frac{e_i}{p_i}$
Necessity: Schedulable -> Total Utilization <= 1
증명 대상:
만약 총 이용률 $U=\sum_{i=1}^{n}\frac{e_i}{p_i} > 1$이라면, Task Set은 EDF로 절대 스케줄링 될 수 없다.
- 가정: $\sum_{i=1}^{n}\frac{e_i}{p_i} > 1$
- 각 작업 $\tau_i$는 매 $p_i$초마다 도착 -> 1초에 각 작업이 차지하는 CPU 시간은 $\frac{e_i}{p_I}$
- 전체 작업이 1초 동안 요구하는 CPU 시간의 합:
- $$U=\sum_{i=1}^{n}\frac{e_i}{p_i} > 1$$
- 즉, 단위 시간 내에 CPU가 해야 하는 작업량 > 1초
- 단일 CPU는 단위 시간에 최대 1초만 일할 수 있음
- CPU는 시간 내에 모든 작업을 완료할 수 없음 -> Deadline 초과 발생
- EDF 실패
Counting Execution Time (Easy Case) - 충분조건

가정:
- $T_{22}$라는 작업이 마감 $t$에서 실패함
- Deadline 실패의 조건: Deadline 이전까지 실행되어야 할 Job들의 총 실행 시간 > t
수식:
$$T_1:\left \lfloor \frac{t-\theta_1}{p_1}\right \rfloor e_1, \,\,\,\,\, T_2:\left \lfloor \frac{t}{p_2}\right \rfloor e_2$$
논리 전개:
1. Deadline 실패 조건:
$$\left \lfloor \frac{t-\theta_1}{p_1}\right \rfloor e_1 +\left \lfloor \frac{t}{p_2}\right \rfloor e_2 > t$$
2. Bound 완화 (floor 함수 제거 -> 상한 이용):
$$\frac{t}{p_1}e_1+\frac{t}{p_2}e_2>t$$
3. 양변을 t로 나누면:
$$\frac{e_1}{p_1}+\frac{e_2}{p_2}>1$$
Counting Execution Times (Difficult Case) - 충분조건
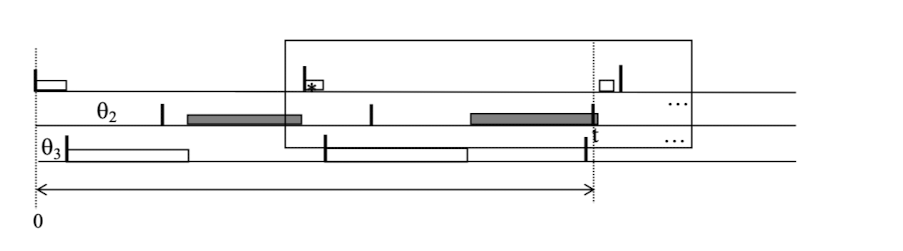
위와 같은 경우, 앞 선 예제와 같이 t에 대한 깔끔한 수식으로 정리할 수 없다.
$$T_1:\left \lfloor \frac{t}{p_1}\right \rfloor e_1 + *, \,\,\,\, T_2:\left \lfloor \frac{t-\theta_2}{p_2}\right \rfloor e_2, \,\,\,\, T_3:\left \lfloor \frac{t-\theta_3}{p_3}\right \rfloor e_3$$
따라서 일반적인 상황에 대한 증명은 아래와 같이 전개한다.
If Job $T_k$ misses deadline at $t$ => $D(t)>t\Rightarrow \sum_{i=1}^{n}\frac{e_i}{p_i}>1$
증명:
- 시간 $[0, t]$까지, 각 작업 $\tau_i$의 인스턴스 수는:
- $n_i(t)=\left \lceil \frac{t-\theta_i}{p_i}\right \rceil$
- 단, $\theta_i$는 작업 $\tau_i$의 첫 도착 시간(offset)
- 이전에는 내림연산을 했는데, 왜 복잡한(일반적인) 증명에서는 올림을 썼는가?
- Deadline 실패가 일어났음을 근거로, 어쨌든 이 시간까지 처리됐어야 했던 최소 요구량을 보수적(최악의 경우로) 상정해야 했기 때문이다.
- EDF에서는 Deadline 순서가 중요하기 때문에, 앞 서 마감되는 job들이 t까지 완료되어야만 대상 job이 시간 안에 완료될 수 있음
- 따라서 interference의 upper bound를 구할 때는 올림 연산을 쓴다.
- 해당 시간까지의 CPU 요구향:
- $D(t)=\sum_{i=1}^{n}n_i(t)\cdot e_i$
- 마감이 실패했다면, 반드시 CPU가 이 요구량을 다 처리하지 못한 것이므로:
- $D(t)>t$
- 다음 부등식을 위해 $n_i(t)\geq \frac{t-\theta_i}{p_i}$을 이용:
- $D(t)=\sum_{i=1}^{n}n_i(t)\cdot e_i \geq \sum_{i=1}^{n}(\frac{t-\theta_i}{p_i})\cdot e_i$
- $=\sum_{i=1}^{n}(\frac{t}{p_i}-\frac{\theta_i}{p_i})e_i=t \cdot \sum_{i=1}^{n}\frac{e_i}{p_i}-\sum_{i=1}^{n}\frac{\theta_ie_i}{p_i}$
- 따라서 마감 실패라면:
- $t\sum_{i=1}^{n}\frac{e_i}{p_i}-\sum_{i=1}^{n}\frac{\theta_ie_i}{p_i}>t$
- 정리파면:
- $t\cdot(\sum_{i=1}^{n}\frac{e_i}{p_i}-1)>\sum_{i=1}^{n}\frac{\theta_ie_i}{p_i}$
- 우변은 상수이므로, 좌변이 양수이기 위한 조건은:
- $\sum_{i=1}^{n}\frac{e_i}{p_i}>1$
복잡한 시니라오를 Lemma들을 이용하여 간단한 시나리오처럼 변경하여 증명하기
Lemma 1: Idle Interval Lemma
어떤 시점 $t$에서 CPU가 idle이었다가 다시 바빠지기 시작했다면, 그 $t$이후의 스케줄링은 이전의 작업들과 무관하게 독립적으로 분석 가능하다
- 즉, 시점 $t$를 새로운 시간 0으로 삼고, 그 이후만 보면 된다.
- 그 이전에 실행된 Job들은 Deadline 실패에 아무런 영향을 주지 않음
결론:
이전 Job의 잔재는 없고, 새로운 시점부터 분석하면 패턴을 단순화할 수 있다.
Lemma 2: Busy Interval Lemma
어떤 작업 $T_k$가 Deadline $t$에 실패했다고 가정할 때, 그 Job의 Release 시점부터 $t$까지 중 마지막 idle time 이후 구간을 찾으면, 그게 바로 최신 busy interval이다.
- busy interval은 CPU가 계속 바쁘게 돌아간 시간 구간
- 이 구간의 시작점을 새로운 시간 0으로 삼아도 분석 결과가 동일
결론:
복잡하게 얽힌 과거 스케줄링 이력을 잘라내고 무시할 수 있음 -> 깔끔한 상태로 재분석 가능
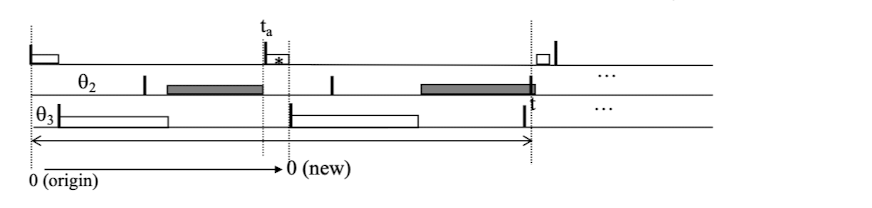
- 앞서 위에서 살펴봤던 그래프를 다시 살펴보면, 기존의 Idle interval Lemma를 좀 더 확장해서 적용할 수 있다.
- 기존의 Idle interval Lemma는 모든 CPU가 idle한 상태라면, 그 이후의 스케줄링은 idle 이전 스케줄링과 독립적이라는 말이다.
- 이 그래프에서는 * Job이 실행할 수 있었다는 것 (그 시점에 상대 Deadline이 가장 멀다)은 $t_a$ 시점까지 CPU가 비워져있었다라고 볼 수 있다.
- 이건 암묵적으로, EDF 정책에 따라 $t_a$ 시점 이전에 마감이 더 이른 Job이 모두 완료되었음을 의미한다.
- 즉 해당 구간은 "간접적으로 idle"이라고 볼 수 있다. -> 더 급한 작업이 없었기 때문에 *를 실행할 수 있었다.
- 그래서 $t_a$를 새로운 시간 0으로 설정하면,
- 그 이전의 간섭은 제거 가능
- 이후의 Job은 이전의 Job의 영향을 받지 않음

자 이제, 우리는 $t_a$를 새로운 0으로 지정하였고, 맨 처음 규칙대로 시작 시점부터 첫 Release 시점까지를 $\theta$로 두고 계산하면 아래와 같다.
$$T_1:\left \lfloor \frac{t-\theta_1}{p_1}\right \rfloor e_1 < 0 \,\,\,\,Ignored!,\,\,\,\,\,T_2:\left \lfloor \frac{t-\theta_2}{p_2}\right \rfloor e_2,\,\,\,T_3:\left \lfloor \frac{t}{p_3}\right \rfloor e_3$$
Time-Demand Analysis
EDF 스케줄링이 안전한지 확인하고 싶은데, 모든 arrival pettern을 다 체크할 수는 없자나? 그런데 최악의 경우 하나만 체크해도 된다고?
Time-Demand Analysis
실제 시간 축을 따라 Demand와 Supply 비교
- Time-Demand: 일정 시간동안 모든 Job들이 요청한 CPU 시간의 총합
- Time-Supply: 그 시간동안 CPU가 제공 가능한 시간 (보통 t초라면 t)
아이디어:
시간 $t$까지 Demand <= Supply가 항상 성립하면 스케줄 가능
문제:
그걸 모든 시점, 모든 도착 패턴에 대해 무한히 확인할 수는 없음
Worst-Case Pattern with EDF
EDF에서는 "모든 경우"를 확인하지 않아도 된다.
정리: 만약 어떤 Task Set에서 마감 실패가 생긴다면, 반드시 "모든 Job이 동기적으로 도착"하는 경우에도 실패가 발생함
이 동기화된 도착 패턴이 최악의 경우를 만든다.

그림에서 첫번째 패턴은 도착 패턴(Release Pattern)이 동기화되지 않은 상황에서 Deadline Miss가 발생한 모습이다.
두번째 그림은 도착 패턴을 동기화했을 때이고, 이 때도 마찬가지로 Deadline Miss가 발생함을 알 수 있다.
FPS의 Critical Instant와 비교해보면, CI의 경우에는 가령 내가 $T_3$의 CI를 통해 Response Time Analysis를 한다고 할 때, $T_3$보다 우선 순위가 높은 가령 $T_1$, $T_2$만 놓고 분석하면 된다. 다시 말하면 Task마다 별도로 계산할 필요가 있다는 것이다.
반면에 EDF의 Worst Case Pattern의 경우에는 전체 시스템을 기준으로 보기 때문에 전역적 분석 방식이라고 볼 수 있다.
Finite Check
EDF는 최악의 경우에도 일정 시간 구간만 검사하면 전체 스케줄 가능성을 판별할 수 있다.
근거1. Hyperperiod의 반복성
- Hyperperiod = 모든 Job 주기의 최소공배수
- Task Set이 주기적이면, Hyperperiod마다 Job arrival pattern이 정확히 반복된다.
만약 $[0,Hyperperiod]$ 동안에 모든 Deadline이 지켜졌다면,
그 이후도 같은 스케줄이 반복되므로 무조건 성공한다.
근거2. Idle Time Lemma (Processor Becomes Idle)
- 시스템이 완전히 Idle해지는 시점이 있다며, 그 이후는 마치 새로운 시스템이 시작되는 것처럼 독립적으로 분석 가능
$[0, First\,\,\,Idle\,\,\,Time]$까지 모든 마감이 충족되었고, Idel 이후에 다시 시작할 수 있다면, 전체 스케줄링은 가능
따라서 결론적으로 우리는 아래 구간만 보면 된다.
$$[0,min(first\,\,idle\,\,time,\,\,hyperperiod)]$$
이 안에서 Deadline 실패가 없으면, 그 이후도 반복이거나 독립적으로 리셋되므로 전체 시스템은 스케줄 가능하다.
Time-demand approach
어떤 Task Set이 EDF로 스케줄링 가능하려면, 모든 시간 구간 $[0,L]$에 대해 CPU가 제공할 수 있는 시간 $L$이 그 시간 동안 요구된 총 Task 실행 시간보다 크거나 같아야 한다.
$$L\geq D[0,L]=\sum_{i=1}^{n}\left \lfloor \frac{L}{p_i}\right \rfloor \cdot e_i$$
- $L$: 분석하고자 하는 시간 간격의 길이
- $D[0,L]$: 시점 0부터 $L$까지의 총 processor demand (요구된 실행 시간)
조건:
Task Set은 다음 조건을 만족해야 한다:
$$\forall L\in [0,min(idle time, hyperperiod)],\,\,\,\,L\geq D[0,L]$$
-> 이게 성립하면 모든 Deadline은 지켜진다. -> 스케줄 가능
Do we really need to check the processor demand for every L?
- 시간 $L$은 이론적으로 무한하다.
- 그래서 실제로는 모든 $L$을 확인하지 않고도 판별 가능한 조건들이 존재한다.
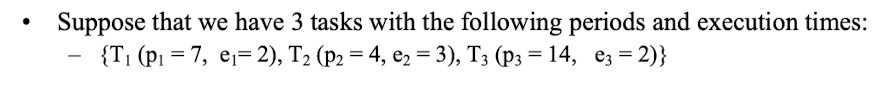
기본적으로 전체 Utilization Bound를 분석해보면,
$T_1 = 2/7$, $T_2 = 3/4$, $T_3=2/14$로 전체는 1.18이다.
자 processor demand approach(time demand approach) 를 적용해보자.
- L=4: $D[0,4]$ = 3 ($T_2$만 계산됨) < L
- L=7: $D[0,7]$ = 5 < L
- L=8: $D[0,8]$ = 8 = L
- L=12: $D[0,12]$ = 11 < L
- L=14: $D[0,14]$ = 15 > L
D[0,14] > 14이므로 Deadline Miss를 찾았다.

Time-Demand Approach와 Classic EDF Schedulability Condition (U <= 1)의 수학적 동치
우리가 알고 있던 "$\sum \frac{e_i}{p_i}\leq 1$이면 스케줄 가능하다"는 Time-Demand 수식으로도 표현할 수 있다.
증명 목표:
$$U=\sum_{i=1}^{n}\frac{e_i}{p_i}\leq 1\,\,\,\,\Leftrightarrow \,\,\,\,L\geq \sum_{i=1}^{n}\left \lfloor \frac{L}{p_i}\right \rfloor \cdot e_i \,\,\,\,(for\,\,all\,\,L\,\,\geq 0)$$
1번 방향
$$U=\sum_{i=1}^{n}\frac{e_i}{p_i}\leq 1\,\,\,\,\Rightarrow \,\,\,\,L\geq \sum_{i=1}^{n}\left \lfloor \frac{L}{p_i}\right \rfloor \cdot e_i $$
if U <=1, then for all L (L>=0)
$$L\geq UL=\sum_{i=1}^{n}\frac{L}{p_i}e_i\geq \sum_{i=1}^{n}\left \lfloor \frac{L}{p_i}\right \rfloor \cdot e_i$$
2번 방향
$$U=\sum_{i=1}^{n}\frac{e_i}{p_i}\leq 1\,\,\,\,\Leftarrow \,\,\,\,L\geq \sum_{i=1}^{n}\left \lfloor \frac{L}{p_i}\right \rfloor \cdot e_i$$
증명방식: 귀류법 (Proof by Contradiction)
1. 가정: $U > 1$
$$\sum_{i=1}^{n}\frac{e_i}{p_i}>1$$
그러면, "어떤 $L$"에서는 Demand가 Time을 초과할 수 밖에 없을 것이라는 직관을 가지고 증명한다.
2. 특정한 $L$ 선택:
$$L=lcm(p_1,p_2,...,p_n)$$
이 $L$에서는 모든 Job이 정수 배수로 정확히 $\frac{L}{p_i}$만큼 도착하게 되므로,
$$\left \lfloor \frac{L}{p_i}\right \rfloor = \frac{L}{p_i}$$
따라서 processor demand는:
$$D[0,L]=\sum_{i=1}^{n}\left \lfloor \frac{L}{p_i}\right \rfloor \cdot e_i = \sum_{i=1}^{n}(\frac{L}{p_i}\cdot e_i)=L\cdot U$$
3. 그런데 1번 가정과 같이 $U>1$ 이라면
$$L\cdot U > L\Rightarrow D[0,L]>L$$
즉, Demand > Available time -> Deadline miss 발생
Time-Demand Analysis가 왜 필요한가?
이미 우리는 U<=1과 같은 스케줄 가능성을 확인하는 방법이 있는데 왜 굳이 복잡한 Time-Demand/ Processor-Demand Approach가 필요할까?
Utilization Bound는 단순하고 계산이 쉽지만,
Period == Deadline이 경우에만 필요충분조건이 성립한다.
이런 경우에는 Time-Demand/Processor-Demand Approach가 효과적이다.
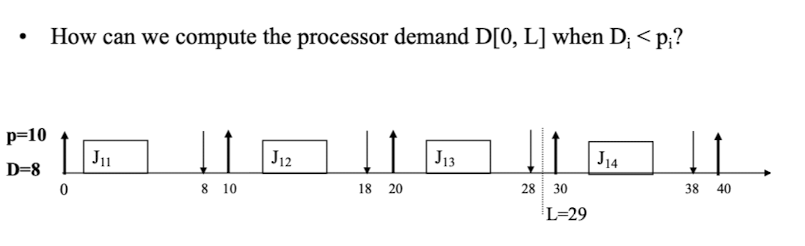
기존 공식대로 계산하면
$$D[0,L]=\left \lfloor \frac{29}{10}\right \rfloor = 2$$
* Execution Time이 없으므로, 위와 같이 계산 시, L까지 2번 Job이 수행되어야함을 요구하는 것으로 계산되었으나 실제는 3번 수행되어야 한다.
기준점을 Deadline만큼 당겨서 계산하자

- Deadline이 Period보다 짧을 경우, Deadline 기준으로 생각하면 Demand를 정확하게 셀 수 있다.
- 그래서 시작점을 $D_i$만큼 왼쪽으로 이동시켜서:
$$D[0,L]=\sum_{i=1}^{n}\left \lfloor \frac{L-D_i}{p_i}\right \rfloor \cdot e_i$$
문제는 첫번째 job의 Demand가 빠진다.
첫 Job 보정하기
첫 Job이 빠진 부분을 +1 보정으로 해결
$$D[0,L]=\sum_{i=1}^{n}(\left \lfloor \frac{L-D_i}{p_i} \right \rfloor +1)\cdot e_i$$
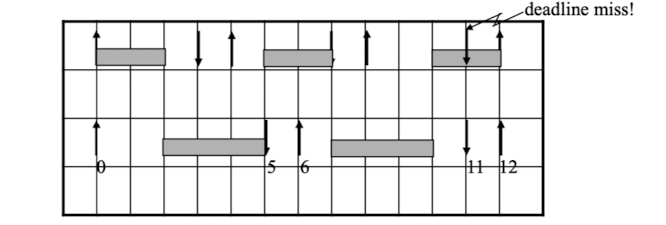
Total Utilizaiton Bound는 1이다.
그런데 과연 스케줄 가능할까?
- L = 5: $D[0,5]$ = 5 = L
- L = 7: $D[0,7]$ = 7 = L
- L = 11: $D[0,11]$ = 12 > L
-> 검사할 L 후보를 뽑는 방법은 Deadline 시점이기 때문이다.
Deadline Miss!
'Study > Real Time Systems' 카테고리의 다른 글
| WCET Analysis (1) | 2025.06.09 |
|---|---|
| Priority-Driven Scheduling of Periodic Tasks (Dynamic Priority) - 2 (1) | 2025.06.08 |
| Scheduler라는 개념은 왜 필요한가? (0) | 2025.05.12 |
| RTS 환경 하에 Mutex, Semaphore 그리고 Spinlock 비교 (0) | 2025.04.22 |
| Reference Model (0) | 2025.04.20 |


