| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- GeorgiaTech
- 개발자
- backtrader
- 암호화폐
- 백트레이더
- 비트코인
- 파이썬
- it
- backtest
- 자동매매
- 확률
- 블록체인
- AWS
- 퀀트
- TOEFL
- AUTOSAR
- 토플 라이팅
- 프로그래밍
- 클라우드
- 토플
- 아마존 웹 서비스
- Bitcoin
- can
- 오토사
- toefl writing
- probability
- 자동차sw
- 백테스트
- Cloud
- python
- Today
- Total
Leo's Garage
Probability and Statistics II: Random Variables – Great Expectations to Bell Curves - 2 본문
Probability and Statistics II: Random Variables – Great Expectations to Bell Curves - 2
LeoBehindK 2023. 12. 13. 22:55Discrete Random Variables
probability mass function (pmf)
Definition: If X is discrete RV, its probability mass function(pmf) is f(x) = P(X = x).
Note that 0 <= f(x) <= 1, sigma f(x) = 1.
pmf는 즉, RV가 이산 RV일 경우에 확률 함수를 의미한다.
따라서 pmf를 전부 더 하면 그 값은 1이 된다.
Uniform distribution의 경우는, X가 각각 1, 2, ... , n 일 때, 각 확률이 1 / n인 확률함수를 의미한다.
Binominal distribution
Definition: Let X denote the number of "successes" from n independent trials such that the P(success) at each trial is p (0 <= p <= 1).
Then X has the Binominal distribution with parameters n and p.
The trials are referred to as the Bernoulli trials.
모든 시행이 독립시행인 사건을 n번 수행하고, 특정 수행이 성공할 확률이 p인 X에 대해서 X는 n과 p에 대해서 Binominal distribution을 가진다고 말한다.
커리가 자유튜를 성공할 확률은 89.5%이다.
커리가 자유투를 10번 수행해서 2번 성공 할 사건에 대해서 우리는 Binominal distribution이라고 하며, 이러한 시행을 Bernoulli trials라고 한다.
Poisson distribution

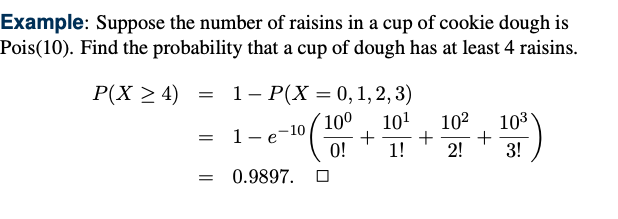
푸아송 분포의 정의는 위와 같다.
확률 함수에 e가 포함되어 있다.
푸아송 분포에 대해 알기 전에 모수(population parameter)를 먼저 이해해야 한다.
모수란 "모집단의 특성을 나타내는 수치"이며, 푸아송 분포에서 모수는 "단위시간 또는 단위공간에서 평균발생횟수"를 의미한다.
이 모수를 푸아송에서는 람다로 표기한다.
그러므로 푸아송 분포는 단위시간, 단위 공간에 어떤 사건이 몇 번 발생할 것인가를 표현하는 이산 확률 분포이다.
푸아송 분포에서 확률은 모수에 따라 달라진다.
어떤 사건의 발생횟수가 (모수를 갖는) 푸아송 분포를 따르는 확률과정을 "푸아송 과정 또는 푸아송 프로세스(Poisson Process)"라고 하며 간단히 말하면, 시간에 따라 확률도 변한다고 생각하면 된다. "푸아송 과정"도 시간에 따라 그 확률이 변한다.



