250x250
반응형
Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
Tags
- 클라우드
- Cloud
- 프로그래밍
- 자동매매
- Bitcoin
- 블록체인
- AWS
- 아마존 웹 서비스
- 개발자
- backtest
- 확률
- 토플 라이팅
- can
- 토플
- 파이썬
- backtrader
- 퀀트
- probability
- 백트레이더
- 자동차sw
- 백테스트
- TOEFL
- GeorgiaTech
- 암호화폐
- it
- python
- 오토사
- toefl writing
- 비트코인
- AUTOSAR
Archives
- Today
- Total
Leo's Garage
Probability and Statistics II: Random Variables – Great Expectations to Bell Curves - 23 본문
Study/GTx
Probability and Statistics II: Random Variables – Great Expectations to Bell Curves - 23
LeoBehindK 2023. 12. 27. 00:08728x90
반응형
Standard Conditioning Argument

E[Y] = P(A)인데, 이때 어떤 RV X에 대해서
E[Y|X = x] = P(Y = 1 | X = x) = P(A|X = x). 로 정리가 될 수 있다.

뭔가 더 복잡하게 만든 것처럼 보인다.

이 경우에 위에서 전개한 Standard Conditioning Argument를 이용하여 위와 같이 정리할 수 있다.
중요한건 P(Y <= x)는 cdf 형태라는 점이다.
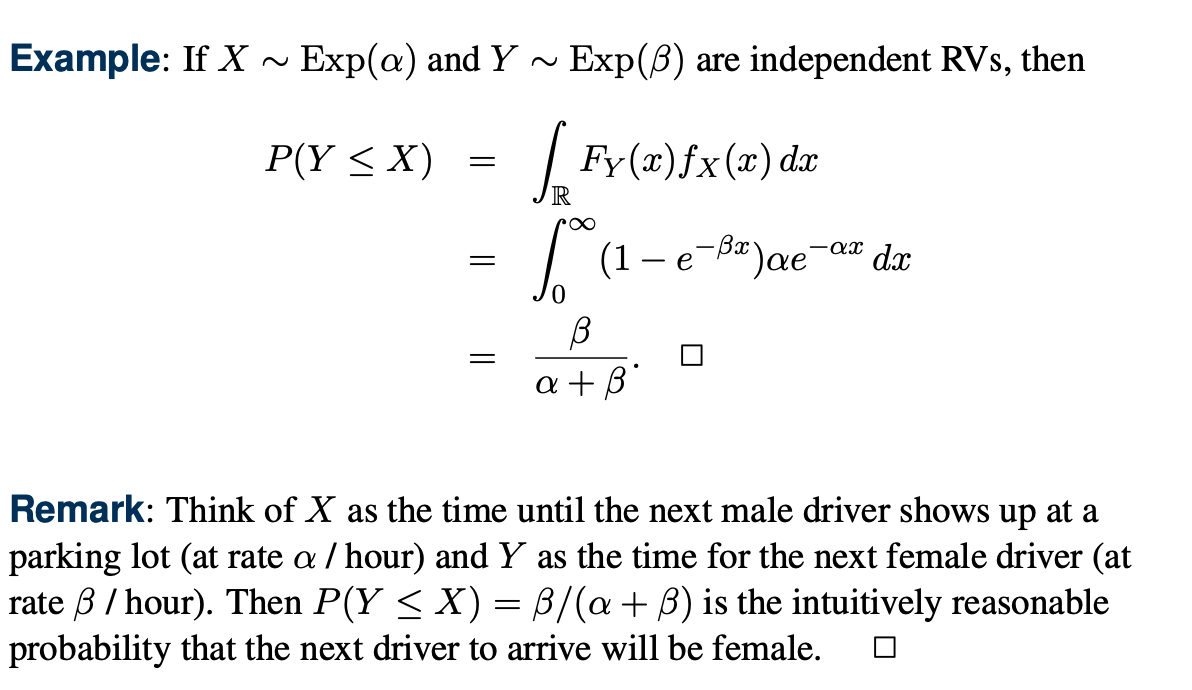
X는 다음번에 남자 운전사가 주차장에 오는 시간에 대한 RV이고, Y는 다음번에 여자 운전사가 주차장에 오는 시간에 대한 RV이 이다.
여기서 a는 시간당 주차장에 오는 남자 수이고, b는 여자 수이다.
직관적으로 P(Y <= X)는 다시 말하면, 여자 운전사가 남자운전사보다 빨리 올 확률을 계산하는 것과 같다.
생각해보면, 어떤 특점 시간을 지정해서 계산하는 것이 아니기 때문이다.
따라서 b/ (a + b) 이다.

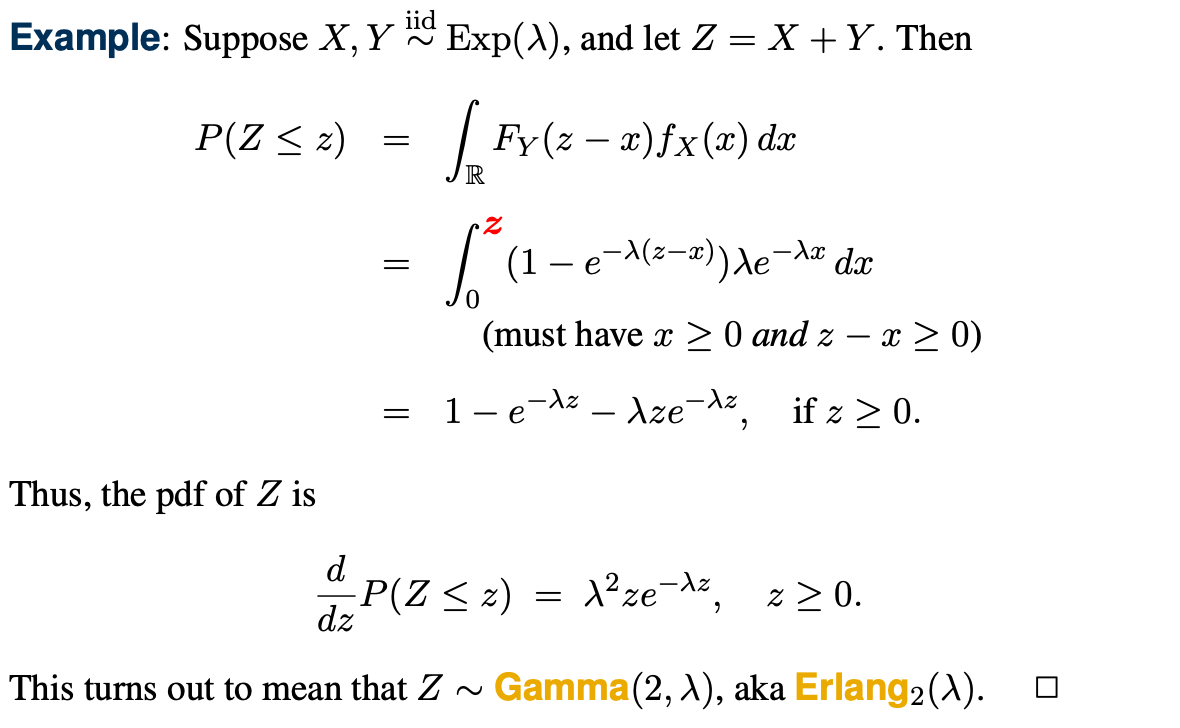


728x90
반응형





