Probability and Statistics II: Random Variables – Great Expectations to Bell Curves - 27

Some Useful Covariance / Correlation Theorems

Covariance에 대한 몇 가지 정리

Var(X + Y) = E[(X + Y)^2] - (E[X + Y])^2를 이용해서 전개할 수 있다. 

서로 독립인 RV간의 Variance 계산

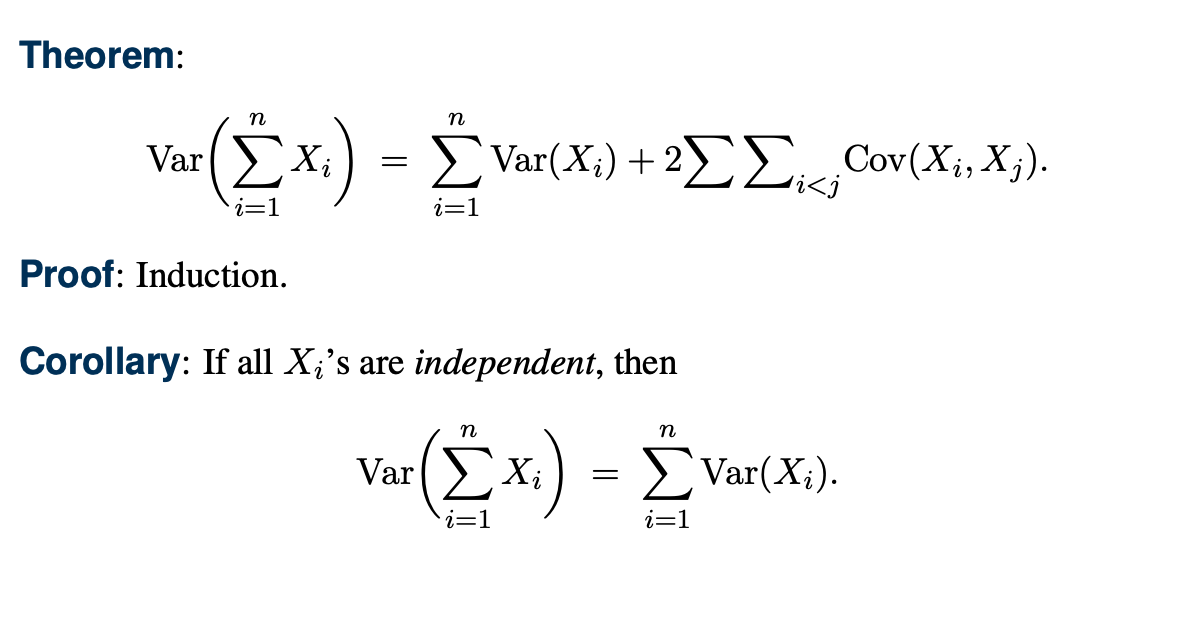
기본적으로 각 RV 자체의 Variance를 구하고, 서로 다른 두 RV간의 Covariance도 계산하여 더한다. 

기본저적으로 Var(X) + Var(Y) + 2Cov(X,Y)를 n개로 확장 전개한 것으로 이해하면된다.

Variance의 특징을 그대로 가진다.

Cov 내에 각 RV의 비례상수의 경우 Cov 계산 시 밖으로 빼서 곱할 수 있다.

n개의 RV에 대한 Variance를 계산할 때도 위와 같이 응용할 수 있다. 

 

위의 공식을 이용한 예제