| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- python
- 실시간시스템
- toefl writing
- Cloud
- 자동매매
- 파이썬
- it
- 클라우드
- 토플
- 확률
- AWS
- TOEFL
- backtrader
- 비트코인
- probability
- 오토사
- 아마존 웹 서비스
- 퀀트
- can
- realtimesystem
- AUTOSAR
- 개발자
- GeorgiaTech
- 블록체인
- 토플 라이팅
- 임베디드
- 암호화폐
- 프로그래밍
- 백트레이더
- 자동차sw
- Today
- Total
Leo's Garage
Scheduling of Aperiodic and Sporadic Jobs in Priority-Driven Systems (Dynamic Priority Framework) 본문
Scheduling of Aperiodic and Sporadic Jobs in Priority-Driven Systems (Dynamic Priority Framework)
LeoBehindK 2025. 6. 9. 15:00앞 선 장에서는 Fixed Priority 스케줄러 기반의 Server에 대해 알아보았다.
이제는 Dynamic Priority에서 Server를 알아보자.
Constant Utilization Server

Key Idea
서버는 $u_s$라는 예산을 받게 되는데, 이는 요청된 Request의 Deadline에 따라서 해당 $u_s$만큼 받는 구조이다.
- 초기화
- $e_s = 0$, $d_s=0$ (서버 예산과 마감시간 초기화)
- 요청 도착 시 (at time $t$)
- Queue가 비어있지 않으면 -> Queue에 추가
- $t<d_s$ (현재 마감시간 이전 도착이면) -> 아무것도 안함 (Queue에 추가만)
- 그 외의 경우
- $d_s=t+\frac{e}{u_s}$
- $e_s=e$(새 요청만큼 서버 예산 설정)
- 현재 시간이 $d_s$가 되었을 때,
- Queue에 요청이 있다면, 맨 앞 요청 처리
- $d_s=d_s+\frac{e}{u_s}$, $e_s=e$
- Queue가 비어있다면 -> 아무것도 안함
- Queue에 요청이 있다면, 맨 앞 요청 처리
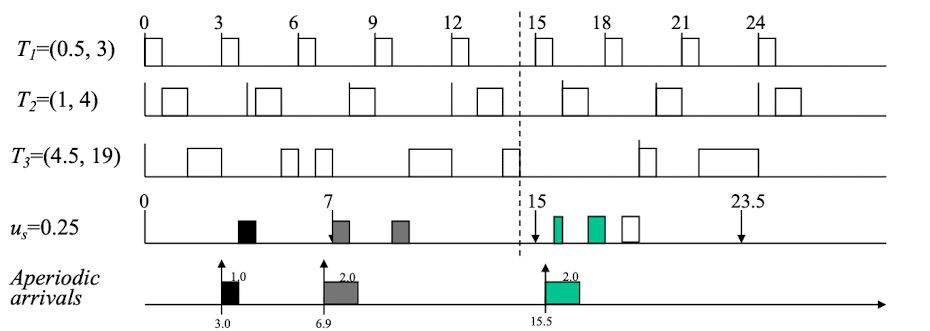
At t = 3, A1 arrives, $e_s$ = 1, $d_s=3 + 4$
At t = 6.9, Nothing
At t = 7, arrives, $e_s$ = 2, $d_s$ = 7+8 = 15
At t = 15, Nothing
CUS 시스템 Schedulability Condition
- Periodic Task들과 일정한 CPU 비율을 사용하는 CUS가 있을 때, 전체 U가 1 이하라면 스케줄 가능하다라는 명제를 증명할 수 있는가?
모순(Contradiction)을 이용한 증명법
목표: U <= 1 이면 스케줄 가능의 반례가 존재하지 않음을 증명
- 총 사용률 <= 1이지만, 특정 작업 $J_{22}$가 Deadline $t$를 넘긴다고 가정
- 그러면 $J_{22}$를 포함한 시간 $[0,t]$ 사이의 계산량 총합이 $t$를 넘겨야 함
- 계산량 식
- $\left \lfloor \frac{t-\theta_1}{p_1}\right \rfloor e_1 + \frac{t}{p_2}e_2 > t$
- $\left \lfloor \frac{t}{p_1}\right \rfloor e_1 + \frac{t}{p_2}e_2 > t$
- $\frac{t}{p_1} e_1 + \frac{t}{p_2}e_2 > t$
- $\frac{e_1}{p_1} + \frac{e_2}{p_2} > 1$
- 이는 전체 이용률이 1보다 크다는 결론이므로 가정에 모순

Counting the Demands

$$d_1 \cdot u_s + d_2 \cdot u_s + d_3 \cdot u_s + e > p$$
$$(d_1 + d_2 + d_3) \cdot u_s + e > p$$
$$\frac{(d_1+d_2+d_3)}{p}u_s+\frac{e}{p} > 1 $$
$$u_s + \frac{e}{p} > 1$$
TBS(Total Bandwidth Server) - Get it done eariler

위의 경우에 $[14,15]$는 현재 Idle time이며, 만약에 3번째 Aperiodic arrival이 $t=14$에 도착한다고 가정하면, CUS는 $t=15$가 될 때까지 idle상태를 유지할 것이다.
Key Idea
CUS와 동일한 방식으로 동작하지만, 보다 이른 시점에 Budget 보충 가능, 마감 시간의 순서는 동일하게 유지되며, Job 도착 시간에 따라 유연한 처리가 가능
- 초기화
- 서버 예산 $e_s=0$, Deadline $d_s = 0$
- 비정기 요청 $e$가 시간 $t$에 도착하면
- Queue가 비어있지 않다면 -> Queue에 요청 추가
- Queue가 비어있고, Server도 대기 중이라면:
- Deadline Update
- $d_s = max(t, d_s) + \frac{e}{u_s}$
- 예산설정
- $e_s = e$
- 즉시 실행 가능
- 비정기 요청 완료 후
- Queue에 요청이 있다면,
- 다음 요청 처리 시작
- $d_s = d_s + \frac{e}{u_s}$
- $e_s = e$
- Queue가 비어있다면 대기
- Queue에 요청이 있다면,

위 그림처럼 CUS는 요청이 들어왔을 때, 이전 요청의 Deadline 이후에 실행이 가능하다, 하지만 TBS의 경우에는 즉시 실행이 가능하다. 따라서 TBS의 경우에는 개별적인 대역폭은 일정하지 않지만, 시스템 전체 대역폭은 일정하다는 것을 알 수 있다.
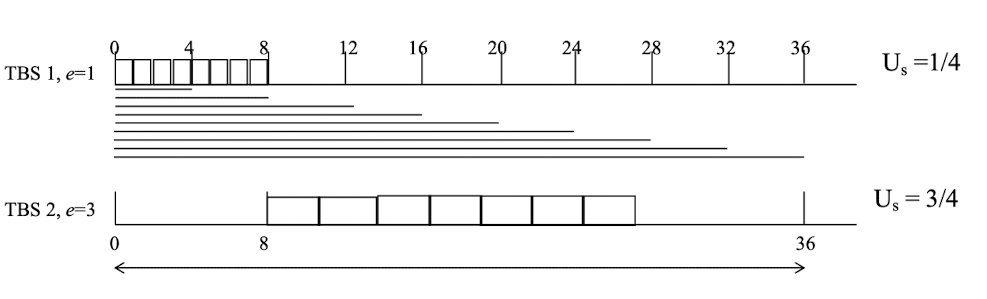
문제는 TBS의 경우 event가 들어오는 족족 Deadline을 업데이트하기 때문에 위와 같은 문제가 발생할 수 있다.
TBS1은 $U_s = 0.25$인데, 총 8개의 요청이 도착했고, 최종적으로 $t=8$시점에 deadline은 36이 되었다. 이때, TBS2는 $U_s=0.75$이어서, 상대적으로 TBS1보다 TBS2의 Deadline이 짧으므로 TBS1은 순간적으로 Starvation 상태에 빠지게 된다.
Fairness
각각 backlogged server는 주어진 시간 동안 서버 크기에 비례하는 CPU 자원을 받아야 한다.
- 이 정의에 따르면, TBS는 전체 시간의 1/4만큼, TBS2는 3/4만큼 CPU를 받아야 공정
- 하지만 실제로는 TBS1이 초반에 너무 많이 받아서 이후에는 기회를 잃어버림
Quick Fix
- TBS는 Deadline을 늦게 설정하는 구조 때문에, 시간이 지날수록 우선순위가 낮아져 불공평해짐
- CUS는 그런 문제는 없지만, 유휴 CPU 자원을 사용할 수 없음
해결책:
When CPU idles, restart all backlogged TBS servers - as if from time 0 again
- CPU가 Idle 상태가 되면
- 모든 서버 이력 초기화
- 각 요청은 현재 시간부터 새롭게 Deadline 설정

CBS(Constant Bandwidth Server)
- TBS/CUS의 한계: TBS, CUS는 비정기 작업의 실행 시간을 사전에 정확히 알고 있어야지 Deadline 계산이 가능하다.
- 하지만 실제 시스템에서는 실행시간이 동적이거나 예측 불가능한 경우가 대부분
문제 발생 가능성
- 서버는 실제 실행시간이 아닌 선언된 실행 시간만 보고 Deadline을 설정
- 실행이 초과되면,
- 서버 예산이 이미 소진되었음에도 Job이 계속 실행됨 ($U_s$를 초과하여 실행)
- 이는 Hard RealTime Job의 Deadline miss를 유발할 수 있음
- TBS/CUS는 EDF로 스케줄링하므로, Deadline 기준으로만 실행됨
해결 필요성
- 비정기 작업이 OverRun하더라도 시스템이 안정적으로 동작하기 위해선:
- 실행 시간을 실시간으로 모니터링 할 수 있는 기법 필요
CBS 핵심 메커니즘
- TBS와 유사하지만, 비정기 작업의 실행 시간 정보가 없어도 동작 가능
- 핵심은 "실행 중 예산을 계속 추적($c_s$)하는 것
주요 개념
- $c_s$: 현재 남은 서버 예산
- $d_s$: 현재 서버 Deadline
- $Q_s$: 최대 예산(최대 실행 가능 시간)
- $P_s$: 서버 주기
- $u_s=\frac{Q_s}{P_s}$: 서버의 Bandwidth
동작방식: 비정기 작업이 실행되면, $c_s$를 줄여가며 모니터링함, $c_s$가 0이 되면, 작업은 일시 중단되거나 새로운 deadline이 설정되어 재시도됨

- 비정기 요청이 도착하면
- 도착 시점이 $t$이면, 예산 $c_s = Q_s$로 초기화, Deadline $d_s = t + P_s$
- 실행 중 예산이 남으면
- 다음 요청은 남은 예산 $c_s$과 동일한 $d_s$로 처리 가능
- Deadline 연장없이 효율 유지
- 예산이 소진되면
- 예산 $c_s = Q_s$로 리필
- 마감시간도 연장 $d_s = d_s = P_s$
CBS 동작 규칙
- 요청 도착 시, 대기 요청이 있다면
- 새 요청은 Queue에 추가됨
- Queue 정렬은 자유로운 정책 적용 가능(FIFO 등등..)
- 예산이 소진되면 ($c_s = 0$)
- 죽시 최대값으로 예산 보충: $c_s = Q_s$
- Deadline은 서버 주기만큼 연장: $d_s=d_s + T_s$
- 요청이 끝나고 Queue에 다음 요청이 있다면
- 남은 예산과 Deadline 유지한 채 다음 요청 실행
- 이는 Deadline 갱신없이도 예산이 재활용되는 형태
- 서버가 Idle 상태에서 새 요청 도착
- 새 요청이 시간 $t$에 도착, 서버는 Idle 상태
- 이 떄 두 경우로 나뉨
- Case A
- $\frac{c_s}{d_s-t} > u_s$ (사용률 초과 위험)
- 현재 예산이 너무 많아서, 남은 시간동안 $u_s$를 초과하게 됨
- 이 경우에는 안전하게 예산을 초기화
- $c_s = Q_s$
- $d_s = t + T_s$
- Case B
- $\frac{c_s}{d_s-t} =< u_s$
- 현재 예산을 그대로 사용해도 서버 사용률 초과하지 않음
- 기존 $c_s$, $d_s$ 유지하고 바로 실행
- Case A
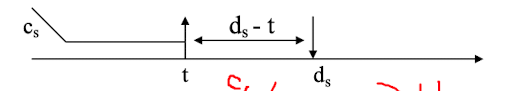
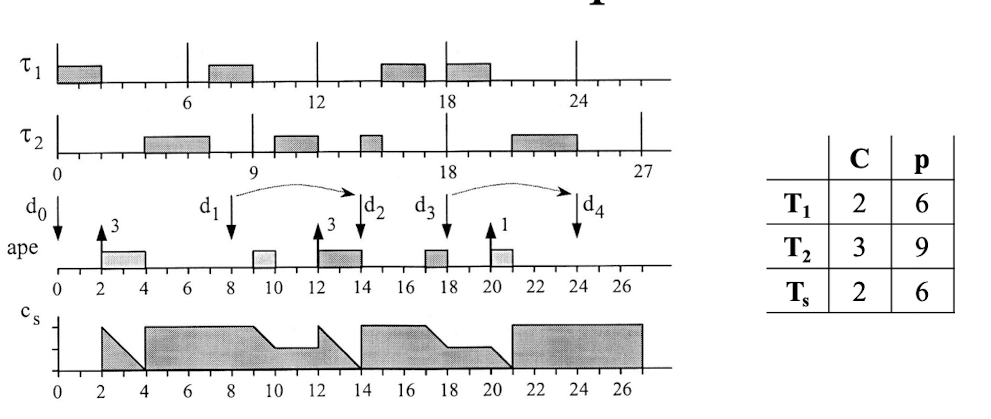
U_s = 2/6 = 0.3?
t = 2, c_s = 2, d_s = 2 + 6 = 8
t = 4, c_s = 2, d_s = 4 + 6 = 10
t = 12, c_s = 2, d_s = 12 + 6 = 18 ($U_s = 1$, 초기화 필요)
t = 14, c_s = 2, d_s = 14 + 8 = 22 (예산 소진)
t = 20 -> $U_s = 0.25 (유지)
t = 21, c_s =2, d_s = 21 + 6 = 29(예산 소진)
Schedulability Analysis of Sporadic Tasks
- 구체적인 deadline이 존재하고, 연속된 두 요청 사이에 최소한의 간격이 존재
Instantaneous Utilization
- 하나의 $J_i$에 대해:
- $utilization = \frac{e_i}{d_i - r_i}$
- $e_i$: 실행 시간
- $r_i$: 도착 시간
- $d_i$: Deadline
- 해당 Job이 실행 가능한 구간 $[r_i,d_i]$동안 Active상태라고 정의
Sporadic Job Theorem
EDF 스케줄링 사용할 때, 다음 조건을 만족하면 Task Set은 스케줄 가능하다
$$\sum_{J_i,\,\,\,\,active\,\,at\,\,time\,\,t}^{}\frac{e_i}{d_i-r_i}\leq 1\,\,\,\,\forall t$$
즉, 모든 시점 $t$에 대해 활성된 작업들의 즉각적 사용률의 총합이 1이하이면, 스케줄링 가능

Sporadic Job Theorem은 충분조건이지 필요조건이 아니다. 즉, 이 조건을 만족하지 않아도 스케줄 가능한 경우가 존재
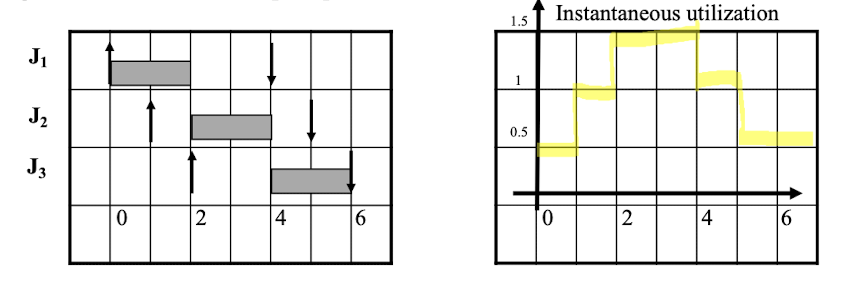
위 그림에서 $J_1$, $J_2$, $J_3$ 전부 $u_i = 0.5$이다.
이때, $t = 2$시점에 3개의 Job에 모두 걸치게 되므로 총 사용률은 1.5가 되어 1을 초과하지만, 실제로는 스케줄 가능하다.
Schedulability Analysis of Sporadic Tasks - Case 1: max instantaneous utilization is known
- 각 Sporadic Task $T_i$는 여러개의 Job $J_{i,j}$로 구성됨
- 해당 Task의 사용률은 아래와 같이 정의됨
- $\bar{u_i}=max_{j}(\frac{e_{i,j}}{d_{i,j}-r_{i,j}})$
- 즉, 각 Job의 실행시간/유효기간 비율 중 가장 큰 값을 사용
Theorem(충분조건)
EDF 기반으로 스케줄링할 때, 모든 sporadic task들의 최대값 사용률 합이 1이하이면 스케줄 가능하다.
$$\sum_{i}^{}\bar{u_i}\leq 1$$
Corollary(추론결과)
주기적 작업과 비정기(Sporadic)작업이 섞인 시스템도, 전체 사용률 합이 1 이하이면 EDF로 스케줄 가능
Case2: Max Instantaneous Utilization을 사전에 알 수 없는 경우
- 실행시간과 Deadline간의 비율을 미리 알 수 없는 상황(실시간 동적 환경)
- 이럴 땐 "Job by Job" 방식의 online admission test가 필요함
Online Admission Test 절차
- 가용 자원 계산
- 주기적 작업이 70% 사용하면, sporadic은 최대 30%까지만 허용
- 활성화된 sporadic job들의 총 즉각적 사용률 추적
- Job 도착 시: 해당 Job의 사용률 총합에 추가
- Job 마감 시: 해당 Job의 사용률 총합에서 제거
- $$\sum_{active\,\,J}^{}\frac{e_i}{d_i-r_i}\leq available \,\,\,bandwidth$$
'Study > Real Time Systems' 카테고리의 다른 글
| Priority-Driven Scheduling of Periodic Tasks (0) | 2025.06.18 |
|---|---|
| Resource and Resource Access Control (only on Fixed Priority System) (1) | 2025.06.09 |
| Scheduling of Aperiodic and Sporadic Jobs in Priority-Driven Systems (Fixed-Priority Framework) (0) | 2025.06.09 |
| WCET Analysis (1) | 2025.06.09 |
| Priority-Driven Scheduling of Periodic Tasks (Dynamic Priority) - 2 (1) | 2025.06.08 |




