| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- Cloud
- toefl writing
- backtrader
- 임베디드
- 클라우드
- 확률
- 자동차sw
- can
- 토플
- AWS
- 백트레이더
- probability
- 개발자
- 파이썬
- TOEFL
- 토플 라이팅
- 자동매매
- it
- GeorgiaTech
- 실시간시스템
- python
- 비트코인
- 퀀트
- 아마존 웹 서비스
- 블록체인
- 오토사
- AUTOSAR
- 프로그래밍
- realtimesystem
- 암호화폐
- Today
- Total
Leo's Garage
Scheduling of Aperiodic and Sporadic Jobs in Priority-Driven Systems (Fixed-Priority Framework) 본문
Scheduling of Aperiodic and Sporadic Jobs in Priority-Driven Systems (Fixed-Priority Framework)
LeoBehindK 2025. 6. 9. 12:59Types of Aperiodic Requests
Soft aperiodic Task:
- 푸아송 분포와 같이 랜덤하게 요청
- 지수 분포처럼 랜덤한 실행 시간
- 일반적으로 User Request를 모델링한다.
Firm aperiodic Tasks(Sporadic Tasks:
- 각각 요청된 Job은 확실한 Deadline 내에 끝나야한다.
- 2개의 연속 요청 사이에는 최소한의 간격이 존재
- WCET Bound가 있다.
- 일반적으로 위급한 상황을 모델링한다.
그렇다면 이런 Aperiodic Task는 어떻게 처리해야 하는가?

1. Interrupt Handling
- 특징: Aperioic Task가 발생 시, 즉시 인터럽트 핸들러에서 처리
- 장점: 매우 짧은 응답 시간
- 단점: Periodic Task가 방해 받아 Deadline Miss 발생 가능
2. Background Service
- 특징: Aperiodic Task는 낮은 우선순위의 Background 작업으로 처리
- 장점: Periodic Task 우선 처리 보장
- 단점: Aperiodic Task 응답 시간이 나쁨
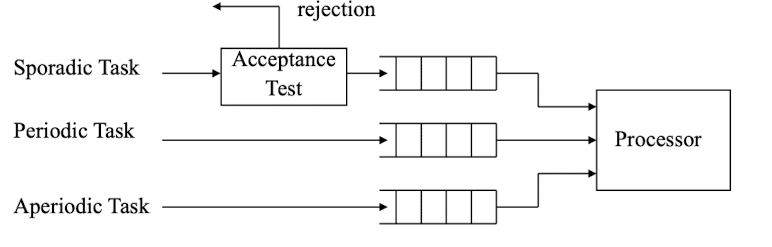
3. Polling Server
- 특징: 일정 시간 간격마다 일정 처리 예산을 가진 Server가 Aperiodic Queue를 검사하고 처리
- 장점: 분석 용이, 실시간성 보장 가능
- 단점: 응답 시간은 Interrupt보다 길지만 BackGound보다 나음, 위 그림처럼 첫 주기에서는 Budget이 없어 처리 불가
$$\sum_{i=1}^{n}\frac{e_i}{p_i}+\frac{e_s}{p_s}\leq (n+1)(2^{1/(n+1)}-1)$$
여기서 n+1인 이유는 기존의 periodic Task n개 + polling server 1개를 더해야 하기 때문에
M/M/1 대기열 모델로 aperiodic 응답 시간 분석:
평균 응답시간:
$$w=\frac{E[S]}{1-\rho}$$
- $E[S]$: aperiodic job 하나의 평균 서비스 시간
- $\rho$: aperiodic job들이 사용하는 평균 대역폭(utilization)
- $\rho=\frac{\lambda E[S]}{1}$
- Polling 서버의 서비스 시간 $\approx 0.5P_s+E[S]$
- 서버가 주기를 기다리는 동안 생기는 지연 포함
Deferrable Server
Polling Server와 Interrupt Handling의 장점을 결합하려는 시도
특징:
- Periodic하게 Budget을 받지만, 언제든지 사용할 수 있도록 보존함(Polling과 차이점)
- 월급처럼 예산은 정기적으로 지급되지만, 사용은 자유롭게

예를들어, $e=50ms$, $p=250ms$의 Deferrable Server가 있다고 하자.
- 매 250ms마다 Budget이 Reset(남은 예산 이월 안됨)
- Request는 Queue에 쌓이고, Queue의 첫 요청이 Budget 유무 확인
Request 처리 방식:
- Budget이 남아있으면:
- 요청이 완료될 때까지 실행하거나,
- 예산이 소진될 때까지 실행 -> 중단 -> 다음 주기까지 대기
- 예산이 없으면:
- 바로 대기 상태로 전환 (다음 주기까지 대기)
| 조건 | 동작 방식 | 유사 방식 |
| 예산 ≫ 요청량 | 거의 중단 없음, 고우선순위면 거의 인터럽트 방식 | Interrupt Handling |
| 예산 ≪ 요청량 | 자주 중단됨, 요청이 큐에서 오래 대기 | Polling |
| 중간 상황 | 시뮬레이션 필요 | — |
Deferrable Server vs. periodic task

Deferable Server의 경우, 위의 아랫쪽 그림과 같이 2개의 Request가 연속으로 실행될 수 있다.
잘 보면, DS의 경우 Budget을 사전에 정의된 Period마다 얻게 되지만, 문제는 aperiodic request가 언제 도착할 지 모른다는 점이다.
따라서 경우에 따라서는 가령 Period가 4이고 Execution Time이 2일 때, Request가 주기의 절반인 시점에 오고 그 다음 Request가 바로 그 다음 주기의 시작시점에 도착한다면, 위의 그림과 같이 수행되면서 다른 Task의 Deadline Miss를 유도할 수도 있게 된다.
Deferrable Server - Preemption 증가 문제
- DS는 기존 Periodic Task보다 더 자주 Preempt할 수 있다.
- 일반 Periodic Task가 하위 우선순위 Task $\tau_i$에 대해 최대 $ \left \lceil \frac{p_i}{p}\right \rceil$번 Preemption
- 그러나 DS는 시작 시점이 Floating이기 떄문에,
- $$ 1+ \left \lceil \frac{p_i}{p}\right \rceil$$
- 이 점은 RMS 기반의 스케줄 가능성 분석 시 반드시 고려해야 하는 사항
- Yao, Mok, and Chen(1995)가 제안
- 수식을 직관적으로 설명하면 다음과 같다.
- $U_s$ -> 0 일 때:
- Bound는 기존 RMS와 거의 동일하게 수렴
- $U_s$ -> 1 일 때:
- Bound는 급격히 감소 -> DS가 전체 CPU를 쓰는 상태
- $U_s$ -> 0 일 때:
Deferrable Server - RMS Utilization Bound
$$U_lub=(n-1)[(\frac{U_s+2}{2U_s+1})^{1/(n-1)}-1]$$
- $U_s=\frac{e}{p}$:DS의 Utilization
- $n-1$:일반 periodic task 수
- 목적: DS가 포함된 시스템이 스케줄 가능한 총 Utilization Bound 계산
Deferrable Server - Time Demand Analysis
주어진 시간 $t$안에 task $tau_i$가 완료 가능한 지 확인
기본 TDA
$$\alpha_i(t)=e_i+(1+\left \lceil \frac{t}{p}\right \rceil)e+\sum_{j=1}^{i-1}\left \lceil \frac{t}{p_j}\right \rceil e_j$$
- $e_i$: Task i의 execution time
- $e$: DS의 예산
- $p$: DS의 주기
- 첫 항: Task 자체 실행
- 둘째 항: DS가 최대 $\left \lceil \frac{t}{p}\right \rceil + 1$만큼 preempt 가능
- 셋째 항: 더 높은 우선순위 periodic task들의 방해 시간
개선된 TDA(시작점 이동 고려)
$$\alpha_i(t)=e_i+(1+\left \lceil \frac{t-e}{p}\right \rceil)e+\sum_{j=1}^{i-1}\left \lceil \frac{t}{p_j}\right \rceil e_j$$
- 아이디어: DS가 최대 $e$시간 만큼 뒤로 이동해 deffered execution을 일으킬 수 있도록, $t-e$로 보정
- 시각적으로는 DS가 맨 마지막 순간에 끼어들 수 있음 -> worst case 고려
여러 DS가 있는 경우
$$\alpha_i(t)=e_i+\sum_{s=1}^{m}(1+\left \lceil \frac{t-e_s}{p}\right \rceil)e_s+\sum_{j=1}^{i-1}\left \lceil \frac{t}{p_j}\right \rceil e_j$$
- $m$: DS의 수
- 각각 DS $s$에 대해:
- $e_s$: 예산
- $p_s$: 주기
- 여러 DS로 인한 합산 preemption 영향 계산

우선 t = 9이며, 9 시점까지의 TDA를 구하려고 한다 .
TDA에 구하기 위해서는 우리는 DS가 얼마나 Preemption하는지 구해야 하는데 기존 수식을 이용하면 아래와 같다.
$$1 + \left \lceil \frac{t}{p}\right \rceil$$ = 1 + 9/4 = 4
시간 보정된 TDA로 계산하면
$$1 + \left \lceil \frac{t-e}{p}\right \rceil$$ = 1 + 2 = 3
보정된 수식에서 정확한 Preemption 횟수를 계산해준다.

TDA 계산방법
- $t=e_i$부터 $p_i$까지 반복:
- $\alpha_i(t) \leq t$ 만족하는 순간:
- 해당 Task는 Schedulable, 이후 $t$는 더 볼 필요없음
- $\alpha_i(t) \leq t$ 만족하는 순간:
- 만약 $t = p_i$까지도 $\alpha_i(t) > t$:
- 해당 Task는 Deadline miss 가능성 -> unschedulabll

Sporadic Server
1. DS vs. SS
문제점: DS의 추가적인 preemption
- DS는 서버 주기마다 무조건 예산을 갱신함
- 이로인해 예상치 못한 시점에 CPU를 점유할 수 있어, Periodic Task의 스케줄 가능성이 줄어든다.
해결책: SS 적용
- Budget을 "사용했을 때만" 보충함
- Budget을 사용하지 않으면, 보충도 없음-> Budget 사용이 Spread Out
- 결과적으로 preemption이 제한되어 스케줄링이 더 예측 가능함
핵심 아이디어
예산 보충은 최소 $p$시간 간격으로만 허용한다.
DS처럼 무조건 주기적으로 갱신하지 않고, SS는 실제 사용 기반으로 주기 제한된 보충을 수행, 그래서 SS는 Periodic Task처럼 다룰 수 있다.
SS의 상태정의
- Active:
- SS가 실행 중이거나,
- SS보다 높은 우선순위의 Task에 의해 Preempt된 상태
- Idle:
- SS도 실행하지 않고, 우선순위도 높은 Task도 없는 경우
- 이 때는 예산 보충 조건이 발생할 수 있음
Budget 보충 매커니즘
- Replenishment Time(RT)
- Budget 보충이 예정되는 시점
- 예산이 처음 사용된 시점 $T_A$에서, 서버 주기 $p_s$이후 시점에 RT 예약
- $$RT = T_A + p_s$$
- Replenishment Amount(RA)
- 그 시점에 얼마만큼 Budget을 보충할 지 계산
- SS가 Idle이 되거나 예산이 모두 소진된 시점 $T_I$에, $[T_A, T_I]$사이에 소비된 예산의 양 만큼을 RA로 설정

최초에 SS는 Budget을 2가지고 있다.(e가 2이므로), t=2에 요청을 받아서 서비스를 처리하고, Active 시점부터 $p_s$만큼 후에 다시 Budget을 받는데, 사용한 만큼이므로 2를 다시 채운다. 이 때, Budget을 채우기 이전에 Request가 왔으므로, Budget을 채우자마자 다시 서비스 처리한다. 이후 다시 $p_s$만큼 이후에 Budget 2를 받는다.
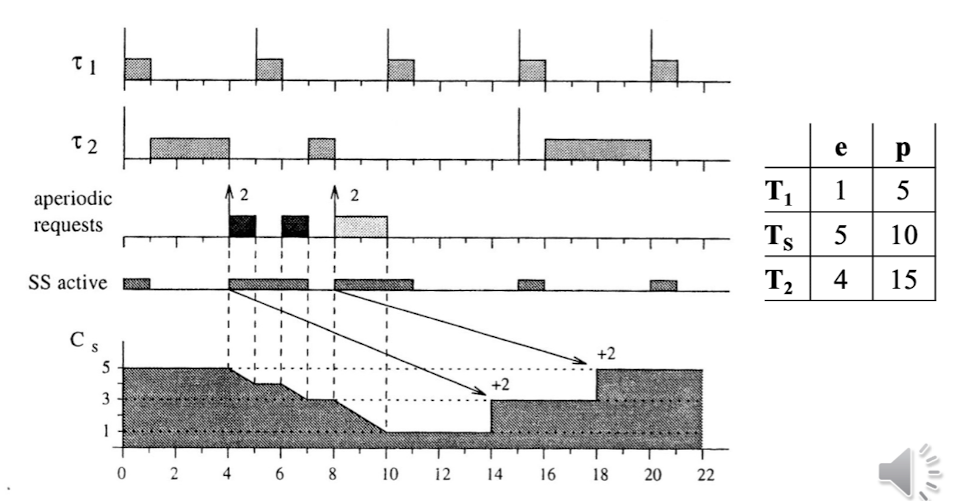
Preemption되는 구간은 Idle구간이 아니다, 따라서 t =4시점에 Active되었고, 그 시점으로 $p_s$만큼 뒤에 Budget을 보충받는데, 최초 Budget은 5였고, 아마도 그림상 요청 당 사용되는 실제 실행 시간은 2로 추정된다(그림이 잘못된 것이 아니라면...)
SS와 Periodic Task는 스케줄링 관점에서 동등하게 다뤄질 수 있는가?
A periodic task set that is schedulable with a task $T_i$ is also scheduable if $T_i$ is replaced by a Sporadic Server with the same period and execution time
즉, 어떤 주기 작업 $T_i = (e_i,p_i)$를 동일한 $e_s, p_s$를 가진 SS로 대체하더라도 전체 시스템의 스케줄 가능성은 보장된다는 이야기이다.
이를 살펴보기 위해서 아래 단계를 진행한다 .
1. 목표: Sporadic Server의 동작이 worst case에서 periodic task와 동등하거나 더 보수적임을 증
증명 논리: $[T_A, T_I]$ 구간 분석
$[T_A,T_I]$: SS가 활성화되고 예산을 사용하는 기간: 이 구간 내에서 SS가 사용하는 방식은 3가지로 분류 가능
Case1 : No Capacity Consumed (예산 미사용)
- SS가 비활성 상태(idle) 상태 유지 -> 간섭없음
- Periodic Task도 같은 조건에서는 실행 안함
- Scheduler 입장에서 차이 없음
Case2: Totally Consumed (예산 완전 사용)
- SS가 전체 예산 $e_s$를 다 소진
- 보충은 $T_A + p_s$까지 기다림 -> 이 동작은 1개 periodic task와 정확히 같다.
- Schedulability 동일
Case3: Partially Consumed (일부만 사용)
- SS가 일부만 실행하고, 나머지는 보존
- 실제 간섭은 더 적다.
- periodic task보다 더 보수적

간단하게 생각해보자.
위 그래프에서 $T_1$은 주기 4에 실행시간 1을 점유하고, $T_2$는 주기 7에 실행 시간 2를 점유한다.
이때 가용한 CPU Time은 주기 5에서 $T_1$의 간섭 2번을 제외한 3이다.
execution Time을 모르는 상태에서 가령 주기 10을 기준으로 DS의 경우 $\left \lceil \frac{t}{p_s}\right \rceil + 1$이므로 3회가 된다.
SS는 +1을 하지 않으므로 2회가 된다.
'Study > Real Time Systems' 카테고리의 다른 글
| Resource and Resource Access Control (only on Fixed Priority System) (1) | 2025.06.09 |
|---|---|
| Scheduling of Aperiodic and Sporadic Jobs in Priority-Driven Systems (Dynamic Priority Framework) (3) | 2025.06.09 |
| WCET Analysis (1) | 2025.06.09 |
| Priority-Driven Scheduling of Periodic Tasks (Dynamic Priority) - 2 (1) | 2025.06.08 |
| Priority-Driven Scheduling of Periodic Tasks (Dynamic Priority) - 1 (1) | 2025.06.08 |




