| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- 파이썬
- 토플
- 블록체인
- toefl writing
- 암호화폐
- AUTOSAR
- GeorgiaTech
- 백트레이더
- backtrader
- 자동매매
- 토플 라이팅
- 퀀트
- 개발자
- python
- 클라우드
- Cloud
- probability
- it
- TOEFL
- 프로그래밍
- realtimesystem
- 비트코인
- 임베디드
- 오토사
- AWS
- 확률
- 자동차sw
- can
- 실시간시스템
- 아마존 웹 서비스
- Today
- Total
Leo's Garage
Priority-Driven Scheduling of Periodic Tasks 본문
Reference Model
실시간 시스템에서 우리는 다음과 같은 Reference Model을 선정할 수 있다.
Periodic Task Model
- $\theta_i$: Phase
- $p_i$: Period
- $e_i$: Execution Time
- $D_i$: Relative Deadline from the beginning of the period.

- 분석의 용이를 위해서 기본적인 가정을 하는 경우가 있는데, $D_i = p_i$로 가정하는 경우가 있다.
여기서는 몇 가지 전제를 하고 이야기를 하려고 하는데
- 모든 Task들은 독립적이다. (서로 공유자원을 사용하지 않는다.)
- 여기에는 aperiodic Task나 sporadic Task가 존재하지 않는다.
- 언제든지 Peemption할 수 있다.
- Context Switching Overhead는 없다고 가정한다.
Priority vs. Criticality
- Priority: 우리가 수행하고자 대기 중인 Job들의 순서
- Criticality (Importance): 만약에 이 Task가 Deadline을 만족하지 못했을 경우에 따른 Panalty 정도
Criticality에 따라서 우선순위를 정할 수도 있지만, 가령 Criticality가 높은 Task의 Deadline이 너무나도 긴 경우에는 이 순서로 우선순위를 정할 필요가 없을 수도 있다.
Ex. 지구에 운석이 떨어지는데 100만년 쯤 뒤라고 하면 이 사건의 우선순위가 높을까? 당장 오늘 내 점심 메뉴를 고르는 일이 우선순위가 높을까?
Priority Scheduling은 Online Scheduling인데, 이유는 Scheduling될 Task들을 Run Time에 결정하기 때문이다. 이와 반대로 Offline에서 이미 순서가 결정된 Scheduler 중 대표적인 예시가 바로 Time Table이다.
버스터미널이나 전철 시간표를 보면 이해가 쉬운데, 이러한 시간표들은 실제로 버스나 전철이 운행되기 전에 결정되어져 있고, 그 시간대로 버스나 전철은 운행될 뿐이다.
반면에 Online Scheduler는 정해진 규칙에 따라 실시간으로 수행할 Task나 Job을 결정한다고 생가하면 된다.
이러한 Online Scheduling 중 우리는 Priority 기반 Scheduler를 살펴보려고 하는데 이 Priority Scheduler도 크게 두 가지로 나눌 수 있는데, Dynamic Priority Scheduler와 Fixed Priority Scheduler이다.
Fixed Priority Scheduler는 각 Task 별로 우선순위가 사전에 정의되어 있고, 이 우선순위가 변경되지 않는다. 가령 Rate Monotonic의 경우를 살펴보면, 자주 불릴 수록 우선순위가 빠른데, 달리 말하면 주기가 짧은 Task일 수록 우선순위가 빠르다라고 말할 수 있다.
반면에 Dynamic Scheduler 중 대표적인 EDF(Earliest Deadline First) Scheduler의 경우, 그 시점에 Deadline이 빠른 Job을 우선적으로 처리한다. 따라서 같은 Task에 있는 Job이어도 시점에 따라 우선순위가 변경될 수 있는 것이다.
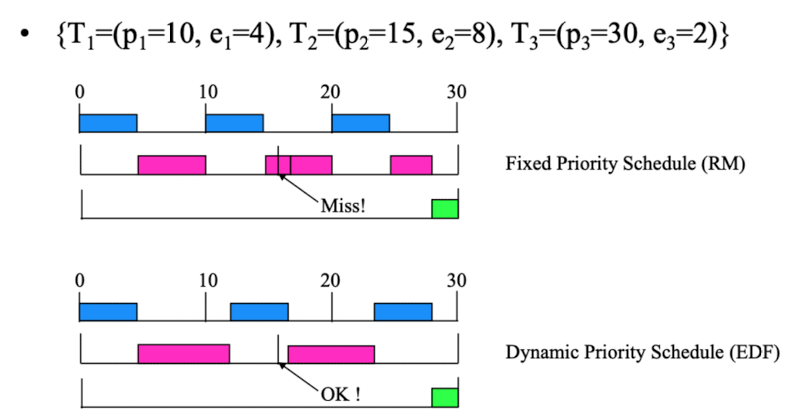
그렇다면, 이러한 Online Scheduling이 Offline Scheduling에 비해 가질 수 있는 장점은 무엇이 있을까?
- 결국 Scheduling에 대한 결정을 Online으로 할 수 있다는 건, flexible하다는 것이다.
- 즉, Task나 Job이 어떤 정해진 시간에 따라 동작할 필요가 없다는 뜻이다.
- Task, Job은 시스템에서 동적으로 진입하거나 나올 수 있다.
그런데 우리는 이런 걱정이 들 수 있다 .
이런식으로 진입과 진출이 동적으로 구성되어버리면, 이 시스템에 대한 Timing Behavior를 어떻게 검증할 수 있을까?
다행히도, 아주 좋은 이론을 이미 여러 사람들이 만들어두었다.
자 그럼 우선 이 이론을 설명하기 앞서서 Static Priority Scheduler에 대해서 좀 더 알아보자.
우선순위를 고정해서 할당함에 앞서서, 우리는 과연 어떤 기준으로 우선순위를 할당할 수 있을까? 물론 우리는 앞에서 Rate Monotonic 방식이라는 것이 있다는 걸 보긴 했지만, 한 번 생각해보자.
아마도, 무작위로 우선순위를 할당하는 방법이 있을 수 있다. - 다만, 이런 방식은 직관적으로 생각하기에도 성능이 매우 떨어질 가능성이 높을 것이다.
두번째로는 기능적 위험도에 따라서 우선순위를 할당할 수도 있는데, 앞 서 언급한 것과 같이 아주 아주 벌어지면 위험한 일도 그 Deadline이 너무 너무 길면, 상대적으로 급하지 않은 일이 될 수도 있다.
세번째로 긴급성이 있다. 위험도와 상관없이 각 Task나 Job이 가지고 있는 Deadline이 존재한다면, 그 기한 안에 해당 Job을 수행해야하는 것은 자명하다. 즉, Deadline이 짧은 Task, Job에 따라 우선순위를 할당하는 것은 자연스럽다.
이렇게 해서 나온 방식이 1. Rate Monotonic(RM), 2. Deadline Monotonic(DM) 방식이다. 전자는 주기를 기준으로 후자는 Deadline을 기준으로 빠른 Task의 우선순위를 높게 할당한다.
이렇게 나온 RM, DM은 일반적으로 Optimal Static Priority Scheduler라고 하는데, 여기서 Optimal의 의미를 이해해야 한다.
어떤 Scheduler S가 Optimal하다는 의미는, 특정 조건 하에서 어떤 Task Set에 대해 Schedulable한 Scheduler가 존재한다면, 이 S도 Schedule 가능하다는 것이다.
혹은 이 Task Set에 대해서 feasible한 Scheduler를 못 찾는다면, 누구도 못찾는다라고 이야기할 수도 있다.
RM은 제한된 조건 하에서 Optimal한 Scheduler인데
- Fixed-Priority Domain
- Deadline == Period
그렇다면, RM이 Optimal하다는 것을 어떻게 증명할 수 있을까?
가장 간명한 방법은 이미 Schedulable한 Task Set에 대하여 Scheduling Policy를 바꿔보는 것이다. 이렇게 해서 Scheduling에 문제가 없다면, RM 역시 feasible한 Scheduler가 될 것이다.
하지만, 문제는 주기 Task에 대해서 무한히 Deadline을 Miss하지 않는지 볼 수는 없다. (시간과 자원이 무한정있지 않기 때문에)
다행히도, 이렇게 하지 않아도 Schedulable한 지 확인할 수 있는 Short Cut이 존재한다.
The Critical Instant Theorem
Static Priority Scheduling을 살펴보면, 어떤 Job이 요청되고 완료하는 시간은 그 해당 Job의 순수한 Execution Time에 그 Job보다 우선순위가 높아서 Preemption되어 들어온 모든 고 우선순위 Job들의 Execution Time의 합으로 계산될 수 있다.
Critical Instant Theorem은 이렇게 Preemption되는 상황 중 가장 Worst Case인 경우가 무엇일지 고민하면서 나온 정리인데, 모든 High Priority Task가 내 Task와 동시에 t = 0 시점에 시작한다면 이 상황이 최악의 상황일 것이다. 따라서 이 조건을 따져보면, 그 이후의 모든 사건들은 이 조건보다 나은 상황이므로 볼 필요가 없다라고 할 수 있다.
이 조건 아래에서 실제 Response Time을 계산하기 위해서는 고려해봐야 할 점이 있는데, 전체 Response Time에 따라서 High Priority Task가 Preemption되는 횟수가 증가할 수 있다는 점이다. 따라서 Response Time은 실제로 계산의 Round가 거듭될 수록 증가되고, 그에 따라서 Preemption도 늘면서 다시 Response Time이 증가할 수 있다.
핵심은 우리가 최초 관심을 가지고 있는 Task의 Deadline까지만 확인하면 되고, 두번째로는 Round를 거듭하였음에도 Deadline 이내의 Response Time이 변하지 않는다면 Schedulable하다고 판정할 수 있다.
$$r_{i}^{k+1}=e_i+\sum_{j=1}^{i-1}\left \lceil \frac{r_i^k}{p_j}\right \rceil e_j, \,\,\,\,where\,\,r_i^0=\sum_{j=1}^{i}e_j $$
- Test terminates when $r_i^{k+1}>p_i$ (not schedulable)
- or when $r_i^{k+1}=r_i^k \leq p_i$ (schedulable)
여기서 하나 생각해야 할 점이 Critical Instant Theorem을 적용할 때, 가령 Task 1, 2 그리고 3에 대해서 Task3가 Schedulable하다고 해서 Task 2가 Schedulable하다고 말할 수는 없다. 따라서 모든 Task에 대해서 확인이 반드시 필요하다.
Time Demand Graph

위와 같은 Task Set이 있다고 가정 할 때,
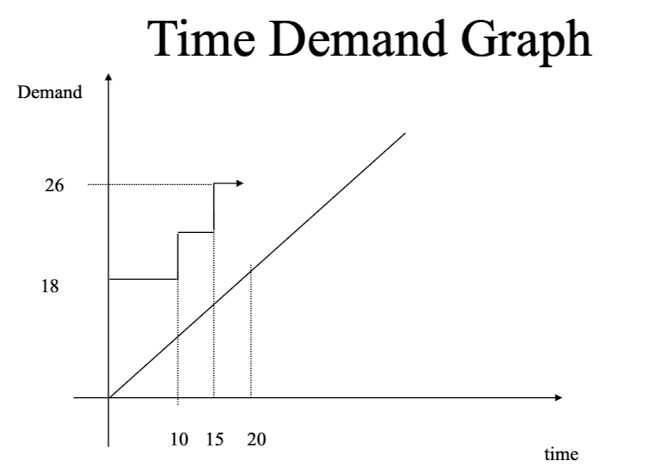
우리는 위와 같은 Time Demand Graph를 그릴 수 있는데, 그리는 방법은 다음과 같다. Critical Instant 조건에서 t = 0에서 10 전 까지는 모든 Task의 Execution Time을 한 번씩 더한 값이 필요하다고 볼 수 있다. 따라서 위 그림에서 x축은 시간이고, y축은 요구되는 시간이다. 시간 10이 되면, Task 1이 한 번 더 실행되고, 15가 되면 Task 2가 한 번 더 실행되는 식이다.
이렇게 분석하는 방법을 Exact Analysis/ Exact Test 라고 부른다.
Utilization
기존에 Exact Test는 강력하긴 하지만, 우리가 모든 Task의 Execution Time과 Period를 알고 있어야만 계산이 가능하다. 그렇다면 우리가 그런 조건을 모른다고 가정할 때도 Schedulable한 지 안 한 지 판단할 수 있는 방법이 없을까?
Utilization은 사용 가능한 전체 시간 대비 실행에 필요한 시간을 나눈 값으로 말 그대로 사용량을 의미한다.
$$U=\sum_{i}^{}\frac{C_i}{p_i}$$
i개의 Task가 존재할 때, 전체 CPU 사용량은 위와 같이 표현할 수 있다.
그렇다면 우리가 소위 특정 Task Set이 Schedulable함을 보장하는 "schedulable utilization bound"를 찾을 수 있을까?
$$if \,\,\,\, \sum_{i}^{}\frac{C_i}{p_i}\leq U_{bound}, \,\,task\,\,set\,\,is\,\,schedulable $$

가령 n개의 Task가 존재한다고 할 때, execution time과 period 조합은 여러가지로 구성될 수 있고, n개의 Task Set 중에서 간신히 Schedulable될 수 있는 Task Set을 찾아서 그 Utilization Bound를 구한다면, n개의 Task Set에 대한 schedulability의 충분조건을 구할 수 있게 된다.
관건은 n개의 Task set이 있을 때, Fixed Priority 조건에서 어떤 조합이 과연 Barely Schedulable한 조합이 될 수 있는지 이다.
좀 더 풀어서 말하면, n개의 Task에는 n개의 execution time과 period가 있을 텐데, 이 조합이 어떻게 구성되어야만 하는지 찾아야 한다.
최대한 U를 줄이는 방향으로 움직여야 하는데,

period가 짧은 task의 execution time 중 일부를 period가 긴 task로 옮기니 U가 작아졌다.
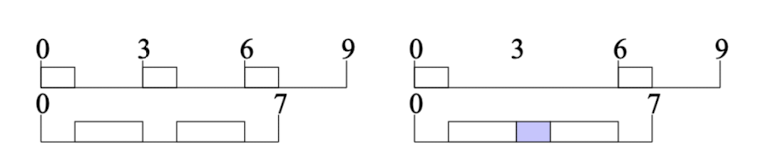
period가 짧은 Task의 execution time을 아래로 내리면서 해당 Task의 주기를 늘리니 U가 작아졌다.
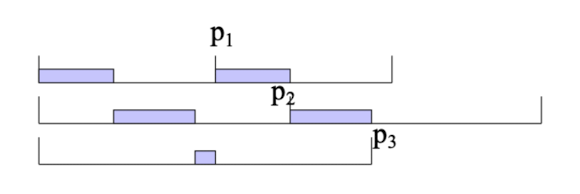
그렇게 해서 찾아낸 Pattern은 다음과 같은데 High Priority Task와 Low Priority Task간의 주기의 비율이 2보다 작아야 한다는 점이다.
$e_1=p_2-p_1;e_2=p_3-p_2;e_{n-1}=p_n-p_{n-1}$
$e_n=p_n-2(e_1+e_2+...+e_{n-1})$
$=p_n-2(p_2-p_1+p_3-p_2+...+p_n-p_{n-1})$
$=2p_1-p_n$
이제 우리는 위와 같은 조건 하에서 Utilization 식을 전개한다.
$U=\frac{e_1}{p_1}+...+\frac{e_n}{p_n}+...+\frac{p_n-p_{n-1}}{p_{n-1}}+\frac{2p_1-p_n}{p_n}$
$=\frac{p_2}{p_1}+\frac{p_3}{p_2}+...+\frac{p_n}{p_{n-1}}+\frac{2p_1p_2...p_{n-1}}{P2...P_{n-1}p_n}-n$
$=r_1+r_2+...+r_{n-1}+\frac{2}{r_1r_2...r_{n-1}}-n;\,\,where\,\,\,r_i=\frac{p_{i+1}}{p_i} $
$set_\partial \frac{\partial U}{r_i}=0$ 최소값이 되는 r을 찾기 위해 편미분했을 때 0이 되는 값을 찾는다.
$r_i^2r_1...r_{n-1}=2$
$r_1=r_2=...=r_{n-1}$
$r=2^{1/n}$
$U=(n-1)2^{1/n}+\frac{2}{2^{(n-1)/n}}-n=n(2^{1/n}-1)$
이것이 바로 Liu & LayLand가 찾아낸 n개의 Fixed Priority Task Set의 Utilization의 Low Bound이다.
이것은 아주 비관적인 수치이기 때문에 실제로는 n개의 Task 조합이 이 U보다 높아도 Schedulable할 수 있다. 다만 이 L&L Bound는 n개의 Task 조합에서 Fixed Priority Task Set일 때, 적어도 이 값보다 U가 작으면 Schedule하는데 문제가 없음을 알려줄 뿐이다.
만약에 우리가 전부 다 알지는 못하지만 일부 정보를 알고 있다면, 그것을 이용해서 더 나은 UB를 구할 수도 있다. 가령 주기를 알고 있다면, 주기는 고정된 값이고 execution time만 변수인 함수가 될 것이다. 최적값을 찾는 여러가지 방법을 통해서 UB를 구할 수 있다.




