반응형
250x250
Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
Tags
- 확률
- 자동차sw
- 프로그래밍
- 자동매매
- backtrader
- Cloud
- AWS
- toefl writing
- 실시간시스템
- probability
- realtimesystem
- 클라우드
- 암호화폐
- AUTOSAR
- 토플 라이팅
- 임베디드
- 백트레이더
- 퀀트
- 비트코인
- python
- 아마존 웹 서비스
- it
- 파이썬
- TOEFL
- can
- 토플
- GeorgiaTech
- 오토사
- 블록체인
- 개발자
Archives
- Today
- Total
Leo's Garage
Probability and Statistics II: Random Variables – Great Expectations to Bell Curves - 9 본문
Study/GTx
Probability and Statistics II: Random Variables – Great Expectations to Bell Curves - 9
LeoBehindK 2023. 12. 23. 18:07728x90
반응형
Some Probability Inequalities

음이 아닌 확률변수가 어떤 양의 실수 이상일 확률의 최소 상계(least upper bound)를 제시하는 부등식이다.
확률과 기댓값의 관계를 설명하고, 확률 변수의 cdf(누적 분포 함수)에 대해 느슨한 경우가 많지만 유용한 한계를 제공한다.
즉, 어떤 양의 실수 이상의 확률 변수에 대해서는 어떤 확률의 이상을 항상 가진다고 말할 수 있다.
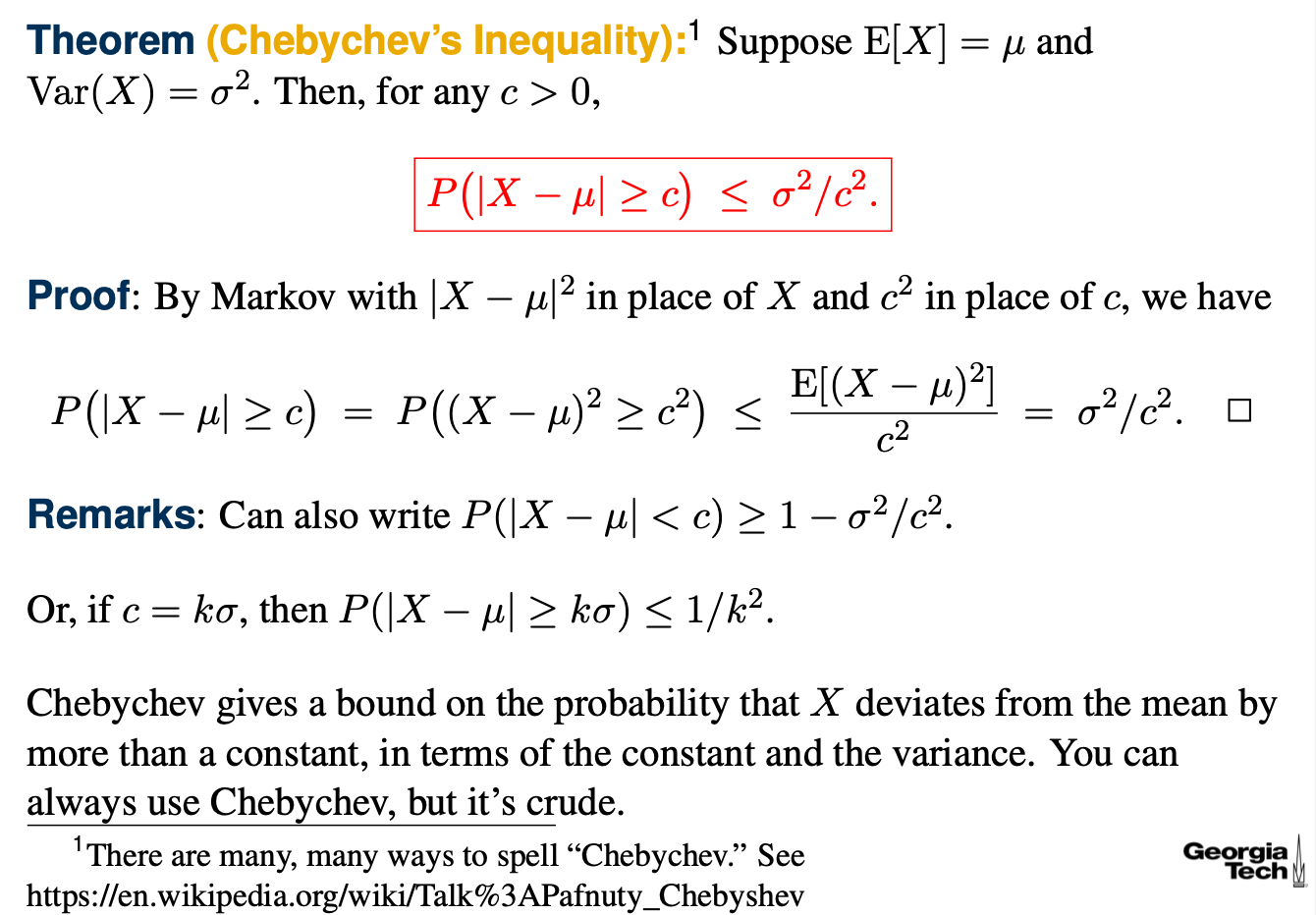
체비쇼프 부등식
확률 분포에서 그 어떠한 데이터 샘플 혹은 확률 분포에서 거의 모든 값이 평균 (mean value)에 근접하며 "거의 모든"과 "근접하는"의 양적 설명을 제공한다.
예를 들어,
- 값 들 중 평균값으로부터 2 표준편차 이상 떨어진 것들은 1/4 이상을 차지하지 않는다.
- 3 표준 편차 이상 떨어진 것들은 1/9 이상 차지하지 않는다.
- 5 표준 편차 이상 떨어진 것들은 1/25 이상 차지하지 않는다.
등등이 있고, 일반적으로는
- 값들 중 평균값으로부터 k 표준 편차 이상 떨어진 것들은 1/k^2 이상 차지하지 않는다.

체르노프 부등식은 확률 변수가 그 기댓값으로부터 벗어날 확률이 항상 크지 않음을 보여준다.
확률 변수의 분포를 알고 있을 때 사용이 가능하고, 체비셰프 부등식에 비해 필요한 정보가 많다.
그리고 mgf를 이용하여 구할 수 있다.
다만, 마르코프 부등식이나 체비셰프 부등식에 비해서 확률변수의 상한값을 오차 없이 제공한다는 장점이 있다.
728x90
반응형




